
【题目】已知A、B、C三点在数轴上的位置如图所示,它们表示的数分别是a、b、c
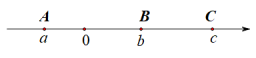
(1) 填空:abc________0,a+b________ac,ab-ac________0;(填“>”,“=”或“<”)
(2) 若|a|=2,且点B到点A、C的距离相等
① 当b2=16时,求c的值
② 求b、c之间的数量关系
③ P是数轴上B,C两点之间的一个动点设点P表示的数为x.当P点在运动过程中,bx+cx+|x-c|-10|x+a|的值保持不变,求b的值
【答案】(1) < , > , > ;(2)①c=10;②c=2b+2;③b=3
【解析】
(1)根据点在数轴上的位置得到a<0<b<c,于是得到结论;
(2)①根据已知条件达到a=-2,b=4,根据点B到点A,C的距离相等,列方程即可得到结论;
②根据![]() 即可判断b、c之间的数量关系;
即可判断b、c之间的数量关系;
③依题意得原式=(b+c-11)x+10a+c当P点在运动过程中,原式的值保持不变,即原式的值与x无关,列方程组即可得到结论.
解:(1)由题中的数轴可知,a<0<b<c,且![]()
∴abc<0,a+b>0,ab-ac>0,
故答案为:<,>,>;
(2) ①![]() 且
且![]() ,
,![]() ,
,
![]() 且
且![]() ,
,![]() .
.
∵点B到点A,C的距离相等,∴![]()
∴![]() ,∴
,∴![]()
②∵![]() , ∴
, ∴![]() ,
,
③依题意,得![]()
![]()
∴原式=![]()
![]()
![]()
∵![]()
∴原式=![]() 【此处
【此处![]() 不取-2没关系】
不取-2没关系】
![]()
∵当 P 点在运动过程中,原式的值保持不变,即原式的值与![]() 无关
无关
∴![]() ,∴
,∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:
“宇番2号”番茄挂果数量统计表
挂果数量x(个) | 频数(株) | 频率 |
25≤x<35 | 6 | 0.1 |
35≤x<45 | 12 | 0.2 |
45≤x<55 | a | 0.25 |
55≤x<65 | 18 | b |
65≤x<75 | 9 | 0.15 |
请结合图表中的信息解答下列问题:
(1)统计表中,a= ,b= ;
(2)将频数分布直方图补充完整;
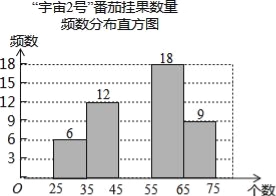
(3)若绘制“番茄挂果数量扇形统计图”,则挂果数量在“35≤x<45”所对应扇形的圆心角度数为 °;
(4)若所种植的“宇番2号”番茄有1000株,则可以估计挂果数量在“55≤x<65”范围的番茄有 株.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE.
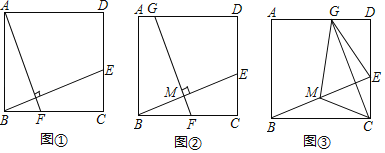
(感知)如图①,过点A作AF⊥BE交BC于点F.易证△ABF≌△BCE.(不需要证明)
(探究)如图②,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(1)求证:BE=FG.
(2)连结CM,若CM=1,则FG的长为 .
(应用)如图③,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某淘宝商家计划平均每天销售某品牌儿童滑板车100辆,但由于种种原因,实际每天的销售量与计划量相比有出入。下表是某周的销售情况(超额记为正、不足记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 | +4 | -3 | -5 | +14 | -8 | +21 | -6 |
(1)根据记录的数据可知该店前三天共销售该品牌儿童滑板车______辆。
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售______辆。
(3)该店实行每日计件工资制,每销售一辆车可得40元,若超额完成任务,则超过部分每辆另奖15元;少销售一辆扣20元,那么该店铺的销售人员这一周的工资总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
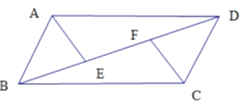
【题目】如图,在口ABCD中,点E、F是对角线BD上的两点,且BF=DE,连接AE、CF.
.求证:AE//CF.
【答案】证明见解析
【解析】试题分析:根据平行四边形的性质可得AD=CB,∠ADE=∠CBF,利用SAS判定△ADE≌△CBF,根据全等三角形的性质即可得∠AED=∠BFC,所以AE∥CF.
试题解析:
∵四边形ABCD是平行四边形,
∴AD=CB,AD∥CB,
∴∠ADE=∠CBF,
又∵DE=BF,
∴△ADE≌△CBF,
∴∠AED=∠BFC,
∴AE∥CF.
【题型】解答题
【结束】
22
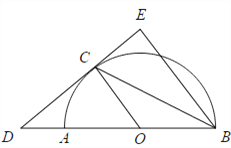
【题目】如图,已知![]() 是
是![]() 的直径,CD与
的直径,CD与![]() 相切于C,
相切于C, ![]() .
.
(1)求证:BC 是![]() 的平分线.
的平分线.
(2)若DC=8, ![]() 的半径OA=6,求CE的长.
的半径OA=6,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 的图象交于A,B两点,已知A点的纵坐标是2.
的图象交于A,B两点,已知A点的纵坐标是2.
(1)求反比例函数的解析式.
(2)将直线![]() 沿x轴向右平移6个单位后,与反比例函数在第二象限内交于点C.动点P在y轴正半轴上运动,当线段PA与线段PC之差达到最大时,求点P的坐标.
沿x轴向右平移6个单位后,与反比例函数在第二象限内交于点C.动点P在y轴正半轴上运动,当线段PA与线段PC之差达到最大时,求点P的坐标.

【答案】(1)![]() ;(2)P(0,6)
;(2)P(0,6)
【解析】试题分析:(1)先求得点A的坐标,再利用待定系数法求得反比例函数的解析式即可;(2)连接AC,根据三角形两边之差小于第三边知:当A、C、P不共线时,PA-PC<AC;当A、C、P不共线时,PA-PC=AC;因此,当点P在直线AC与y轴的交点时,PA-PC取得最大值.先求得平移后直线的解析式,再求得平移后直线与反比例函数的图象的交点坐标,最后求直线AC的解析式,即可求得点P的坐标.
试题解析:
![]() 令一次函数
令一次函数![]() 中
中![]() ,则
,则![]() ,
,
解得:![]() ,即点A的坐标为(-4,2).
,即点A的坐标为(-4,2).
∵点A(-4,2)在反比例函数![]() 的图象上,
的图象上,
∴k=-4×2=-8,
∴反比例函数的表达式为![]() .
.
![]() 连接AC,根据三角形两边之差小于第三边知:当A、C、P不共线时,PA-PC<AC;当A、C、P不共线时,PA-PC=AC;因此,当点P在直线AC与y轴的交点时,PA-PC取得最大值.
连接AC,根据三角形两边之差小于第三边知:当A、C、P不共线时,PA-PC<AC;当A、C、P不共线时,PA-PC=AC;因此,当点P在直线AC与y轴的交点时,PA-PC取得最大值.
设平移后直线于x轴交于点F,则F(6,0)
设平移后的直线解析式为![]() ,
,
将F(6,0)代入![]() 得:b=3
得:b=3
∴直线CF解析式:![]()
令![]() 3=
3=![]() ,解得:
,解得:![]() ,
,
∴C(-2,4)
∵A、C两点坐标分别为A(-4,2)、C(-2,4)
∴直线AC的表达式为![]() ,
,
此时,P点坐标为P(0,6).
点睛:本题是一次函数与反比例函数的综合题,主要考查了用待定系数法求函数的解析式、一次函数与反比例函数的交点坐标,熟练运用一次函数及反比例函数的性质是解题的关键.
【题型】解答题
【结束】
26
【题目】以四边形ABCD的边AB、AD为底边分别作等腰三角形ABF和ADE,连接EB.
(1)当四边形ABCD为正方形时(如图1),以边AB、AD为斜边分别向外侧作等腰直角三角形ABF和ADE,连接EB、FD,线段EB和FD的数量关系是 .
(2)当四边形ABCD为矩形时(如图2),以边AB、AD为斜边分别向内侧作等腰直角三角形ABF和ADE,连接EF、BD,线段EF和BD具有怎样的数量关系?请加以证明;
(3)当四边形ABCD为平行四边形时(如图3),以边AB、AD为斜边分别向平行四边形内测、外侧作等腰直角三角形ABF和ADE,且△EAD与△FBA的顶角都为α,连接EF、BD,交点为G,请用α表示出∠EGD,并说明理由.
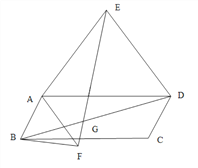
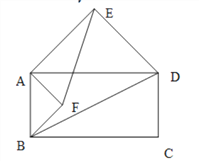

图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在同一平面内,∠AOB=150°,∠COD=90°,OE平分∠BOD.
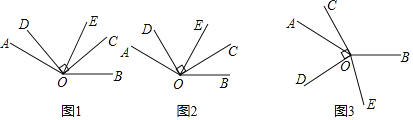
(1)当∠COD的位置如图1所示时,若∠COE=25°,则∠AOD= ;
(2)当∠COD的位置如图2所示时,若∠AOE=90°,则∠AOD= ;
(3)当∠COD的位置如图3所示时,若∠BOE=![]() ∠AOC,求∠AOD的度数.
∠AOC,求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
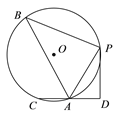
【题目】如图,在⊙O中,B,P,A,C是圆上的点,PB= PC, PD⊥CD,CD交⊙O于A,若AC=AD,PD =![]() ,sin∠PAD =
,sin∠PAD =![]() ,则△PAB的面积为_______.
,则△PAB的面积为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com