
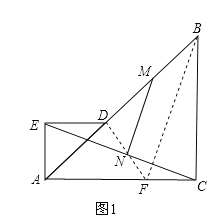
【题目】如图1,△ACB、△AED都为等腰直角三角形,∠AED=∠ACB=90°,点D在AB上,连CE,M、N分别为BD、CE的中点.
(1)求证:MN⊥CE;
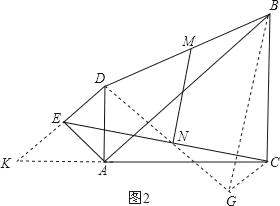
(2)如图2将△AED绕A点逆时针旋转30°,求证:CE=2MN.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)延长DN交AC于F,连BF,推出DE∥AC,推出△EDN∽△CFN,推出![]() ,求出DN=FN,FC=ED,得出MN是中位线,推出MN∥BF,证△CAE≌△BCF,推出∠ACE=∠CBF,求出∠CBF+∠BCE=90°,即可得出答案;
,求出DN=FN,FC=ED,得出MN是中位线,推出MN∥BF,证△CAE≌△BCF,推出∠ACE=∠CBF,求出∠CBF+∠BCE=90°,即可得出答案;
(2)延长DN到G,使DN=GN,连接CG,延长DE、CA交于点K,求出BG=2MN,证△CAE≌△BCG,推出BG=CE,即可得出答案.
试题解析:
(1)证明:延长DN交AC于F,连BF,
∵N为CE中点,
∴EN=CN,
∵△ACB和△AED是等腰直角三角形,∠AED=∠ACB=90°,DE=AE,AC=BC,
∴∠EAD=∠EDA=∠BAC=45°,
∴DE∥AC,
∴△EDN∽△CFN,
∴![]() ,
,
∵EN=NC,
∴DN=FN,FC=ED,
∴MN是△BDF的中位线,
∴MN∥BF,
∵AE=DE,DE=CF,
∴AE=CF,
∵∠EAD=∠BAC=45°,
∴∠EAC=∠ACB=90°,
在△CAE和△BCF中,
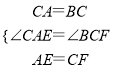 ,
,
∴△CAE≌△BCF(SAS),
∴∠ACE=∠CBF,
∵∠ACE+∠BCE=90°,
∴∠CBF+∠BCE=90°,
即BF⊥CE,
∵MN∥BF,
∴MN⊥CE.
(2)证明:延长DN到G,使DN=GN,连接CG,延长DE、CA交于点K,
∵M为BD中点,
∴MN是△BDG的中位线,
∴BG=2MN,
在△EDN和CGN中,
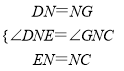 ,
,
∴△EDN≌△CGN(SAS),
∴DE=CG=AE,∠GCN=∠DEN,
∴DE∥CG,
∴∠KCG=∠CKE,
∵∠CAE=45°+30°+45°=120°,
∴∠EAK=60°,
∴∠CKE=∠KCG=30°,
∴∠BCG=120°,
在△CAE和△BCG中,
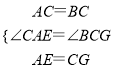 ,
,
∴△CAE≌△BCG(SAS),
∴BG=CE,
∵BG=2MN,
∴CE=2MN.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3,过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2017的横坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为6,点B是数轴上在A点左侧的一点,且A、B两点间的距离为10,动点P从点A出发,以每秒3个单位长度的速度沿数轴向左运动.
![]()
(1)数轴上点B表示的数是 ;
(2)运动1秒时,点P表示的数是 ;
(3)动点Q从点B出发,以每秒2个单位长度的速度沿数轴向右运动,若点P、Q同时出发.求:
①当点P运动多少秒时,点P与点Q相遇?相遇时对应的有理数是多少?
②当点P运动多少秒时,点P与点Q的距离为8个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某日的钱塘江观潮信息如图:

按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离s(千米)与时间t(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点A(0,12),点B坐标为(m,0),曲线BC可用二次函数s=![]() t2+bt+c(b,c是常数)刻画.
t2+bt+c(b,c是常数)刻画.
(1)求m的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以0.48千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为0.48千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度v=v0+![]() (t﹣30),v0是加速前的速度).
(t﹣30),v0是加速前的速度).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系平面内,函数y=![]() (x>0,m是常数)的图象经过A(1,4)、B(a,b),其中a>1,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连接AD,AB,DC,CB.
(x>0,m是常数)的图象经过A(1,4)、B(a,b),其中a>1,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连接AD,AB,DC,CB.
(1)求反比例函数解析式;
(2)当△ABD的面积为S,试用a的代数式表示求S.
(3)当△ABD的面积为2时,判断四边形ABCD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接期中考试,小强对考试前剩余时间作了一个安排,他把计划复习重要内容的时间用一个四边形圈起来.如图,他发现,用这样的四边形圈起来五个数的和恰好是5的倍数,他又试了几个位置,都符合这样的特征。
(1)若设这五个数中间的数为a,请你用整式的加减说明其中的道理.
(2)这五个数的和能为150吗?若能,请写出中间那个数,若不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com