
����Ŀ����ͼ����֪������y��mx2��4mx+3m��m��0����x��Ľ���ΪA��B����y��Ľ���ΪC��DΪ�����ߵĶ��㣮
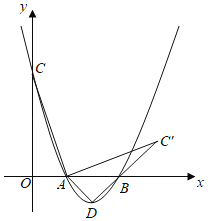
��1��ֱ��д����������C���� ������ ������D���� ������ ����������m��ʾ��
��2����˵������mΪ��ֵ��������һ�������������㲢�����������������ꣻ
��3�������߶�AC�Ƶ�A˳ʱ����ת90��õ�AC�䣬���C������ꣻ
������DC'��AD���Ƿ����m��ʹ�á�ADC��Ϊ���������Σ������ڣ������m���������ڣ���˵�����ɣ�
���𰸡���1��0��3m��2����m����2������������3������C'����Ϊ��1+3m��1����������m��m��ֵΪ��2+![]() ����2��
����2��![]() ��ʱ����ADC��Ϊ���������Σ�
��ʱ����ADC��Ϊ���������Σ�
��������
��1����x=0����õ�C���꣬�������߽���ʽ�����䷽����ö���D���꣮
��2���������߽���ʽ������ʽ�ֽ⣬��y=m��x-1����x-3��������m����0�����Ե���x-1����x-3��������y=0����������߹����㣨1��0���ͣ�3��0����
��3������Ŷ��2����A��1��0������OA=1������C'��x�ᴹ��C'E����֤��AEC'�ա�COA������AE=CO=3m��C'E=OA=1����õ�C'��1+3m��1����
�����������빫ʽ��m��ʾAC'2��AD2��C'D2����AC'��AD��AD��C'D��������ADC'Ҫ��Ϊ���������Σ�ֻ��AC'=C'D���Ѻ�m��ʽ�Ӵ���ⷽ�̼����m��ֵ��
��1����x��0ʱ��y��mx2��4mx+3m��3m
��C��0��3m��
��y��mx2��4mx+3m��m��x��2��2��m
��D��2����m��
�ʴ�Ϊ��0��3m��2����m��
��2��֤����y��mx2��4mx+3m��m��x2��4x+3����m��x��1����x��3��
��m��0
�൱��x��1����x��3����0ʱ��y��0
��ã�x1��1��x2��3
��������һ���������㣨1��0���ͣ�3��0��
��3��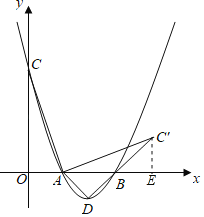
������C'��C'E��x���ڵ�E
���AEC'��90��
�ɣ�2���ɵã�A��1��0����B��3��0��
��OA��1
��C��0��3m��
��OC��3m
�߽��߶�AC�Ƶ�A˳ʱ����ת90��õ�AC��
��AC'��AC����CAC'��90��
���OAC+��C'AE����OAC+��ACO��90��
���C'AE����ACO
�ڡ�AEC'���COA��
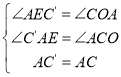
���AEC'�ա�COA��AAS��
��AE��CO��3m��C'E��OA��1
��OE��OA+AE��1+3m
���C'������1+3m��1��
������m��ʹ�á�ADC��Ϊ���������Σ�
��A��1��0����C'��1+3m��1����D��2����m��
��AC'2����1+3m��1��2+12��9m2+1��AD2����2��1��2+����m��2��1+m2��C'D2����1+3m��2��2+��1+m��2��10m2��4m+2
��AC'2��AD2��AD2��C'D2
��AC'��AD��AD��C'D
���ADC��Ϊ����������ʱ��AC'��C'D
��9m2+1��10m2��4m+2
��ã�m1��2+![]() ��m2��2��
��m2��2��![]()
��m��ֵΪ��2+![]() ����2��
����2��![]() ��ʱ����ADC��Ϊ���������Σ�
��ʱ����ADC��Ϊ���������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У�
��![]() ,��
,��![]() ������
������![]() ��һ���㣬��
��һ���㣬��![]() Ϊ�����Ҳ����ȱ�
Ϊ�����Ҳ����ȱ�![]() ����
����![]() ������
��λ�����![]() ��λ�ñ仯���仯.
��λ�ñ仯���仯.
��1����ͼ1������![]() ������
������![]() �ڲ������ʱ������
�ڲ������ʱ������![]() ��
��![]() ��
��![]() ��������ϵ�� ��
��������ϵ�� ��![]() ��
��![]() ��λ�ù�ϵ�� ��
��λ�ù�ϵ�� ��
��2������![]() ������
������![]() �ⲿʱ��(1)�еĽ����Ƿ�������������������֤��������������
�ⲿʱ��(1)�еĽ����Ƿ�������������������֤��������������
��˵������(ѡ��ͼ2��ͼ3�е�һ���������֤����˵��).
(3) ��ͼ4������![]() ���߶�
���߶�![]() ���ӳ�����ʱ������
���ӳ�����ʱ������![]() ����
����![]() ,
,![]() ,���ı���
,���ı���![]() �����.
�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
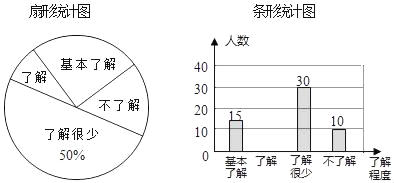
����Ŀ����У��ȫ���ܵ�ȫ���Ĺ㷺��ע������ij��ѧ�Բ���ѧ����У��ȫ֪ʶ���˽�̶ȣ����������������ķ�ʽ���������ռ�������Ϣ����ͳ�ƣ���������ͼ�����в�������ͳ��ͼ���������ͳ��ͼ�����ṩ����Ϣ����������⣺
��1�������ʾ������ѧ�������� ���ˣ�����ͳ��ͼ�����˽�����������Ӧ���ε�Բ�Ľ�Ϊ�� ���㣻
��2��������ѧ����ѧ��900�ˣ���������������������Ƹ���ѧѧ���ж�У��ȫ֪ʶ�ﵽ���˽������������˽����̶ȵ�������Ϊ�� �ˣ�
��3�����Ӷ�У��ȫ֪ʶ�ﵽ���˽����̶ȵ�3��Ů��A��B��C��2������M��N�зֱ������ȡ1�˲μ�У��ȫ֪ʶ������������״ͼ���б������ǡ�ó鵽Ů��A�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺������l��ͼ���Ƶ�P��m��0����ת180�㣬�õ��µĺ���l'��ͼ�����dzƺ���l'�Ǻ������ڵ�P����غ�����
���磺��m��1ʱ������y����x+1��2+5���ڵ�P��1��0������غ���Ϊy������x��3��2��5��
��1����m��0ʱ
��һ�κ���y��x��1���ڵ�P����غ���Ϊ ��
���㣨![]() ����
����![]() ���ڶ��κ���y����ax2��ax+1��a��0�����ڵ�P����غ�����ͼ���ϣ���a��ֵ��
���ڶ��κ���y����ax2��ax+1��a��0�����ڵ�P����غ�����ͼ���ϣ���a��ֵ��
��2������y����x��1��2+2���ڵ�P����غ���y������x+3��2��2����m���� ����
��3����m��1��x��m+2ʱ������y��x2��mx��![]() m2���ڵ�P��m��0������غ��������ֵΪ6����m��ֵ��
m2���ڵ�P��m��0������غ��������ֵΪ6����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����9�֣�Ϊ���� �������Ļ�����ij��λ��չ���������Ļ�֮�����ݽ��������ڰ���1λŮѡ�ֺ�3λ��ѡ�ֵij���˳��ʱ�����������ǩ��ʽ��
��1����ֱ��д����һλ������Ůѡ�ֵĸ��ʣ�
��2�������û���״ͼ���б��ķ�����ʾ��һ����λ����ѡ�ֵ����еȿ��ܽ������������Ƕ�����ѡ�ֵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
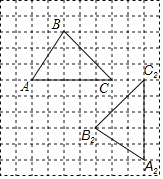
����Ŀ����ͼ���ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������У���ABCΪ��������Σ������������ߵĽ��㣩��
��1������ABC����ƽ��2����λ�õ���A1B1C1���뻭����A1B1C1��
��2������ABC����ij��O��ʱ�뷽����ת90���õ���A2B2C2���뻭����ת����O����ֱ��д���ڴ���ת�����У��߶�ABɨ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ң���1��ͼ��1���������Ρ�6�������κ�6���ȱ���������ɣ���2��ͼ��2���������Ρ�11�������κ�10���ȱ���������ɣ���3��ͼ��3���������Ρ�16�������κ�14���ȱ���������ɣ��������մ˹��ɣ���n��ͼ�������κ͵ȱ������εĸ���֮��Ϊ������������

A.9nB.6nC.9n��3D.6n+3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����MAN=30����������AN��ȡһ��B��ʹAB=4 cm������B��BC��AM�ڵ�C����DΪ��AB�ϵĶ��㣨��D�����A����B�غϣ�������CD������D��ED��CD��ֱ��AC�ڵ�E���ڵ�D�ɵ�A����B�˶������У���AD=x cm��AE=y cm��
��1��ȡָ������ͼ�������������Ԥ��������ͨ����ͼȷ��AD=2 cmʱ����E��λ�ã�����AE�ij��ȣ�
���������⣬�ڴ���ϲ�ȫͼ�Σ�
���ѱ���������ͨ��ȡ�㡢��ͼ���������õ���x��y�ļ����Ӧֵ�������
x/cm | �� |
| 1 |
| 2 |
| 3 |
| �� |
y cm | �� | 0.4 | 0.8 | 1.0 | m | 1.0 | 0 | 4.0 | �� |
��m=______���������һλС������
��2���������ƽ��ֱ������ϵxOy�У�����Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��
��3����ϻ����ĺ���ͼ������⣺��AE=![]() ADʱ��AD�ij���ԼΪ______cm��
ADʱ��AD�ij���ԼΪ______cm��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
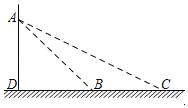
����Ŀ����ͼ��һ���γ��ھ���ij·�ڵĸ�Ӧ��B��C��ʱ�����۵Ƹ��ϵĵ��Ӿ������㵽������Ƭ������Ӧ��֮�����BCΪ6.2m���ڸ�Ӧ��B��C������õ��Ӿ���A�����Ƿֱ�Ϊ��ABD��45������ACD��28��������Ӿ��찲װ�����۵Ƹ��ϵĸ߶�AD�ij����������ȷ��0.1�ף����ο����ݣ�sin28����0.47��cos28����0.88��tan28����0.53��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com