
 ��ͼ���ڡ�ABC�У�AD��BC���ϵĸߣ�BC=12��AD=8������EFGH�ı�EF��BC�غϣ���G��H�ֱ���AC��AB���˶���
��ͼ���ڡ�ABC�У�AD��BC���ϵĸߣ�BC=12��AD=8������EFGH�ı�EF��BC�غϣ���G��H�ֱ���AC��AB���˶������� ��1����FG�ij�Ϊx����AK�ij�Ϊ��8-x����Ȼ����г�����ʽ��$\frac{AK}{AD}=\frac{GH}{CB}$��
��2��������Գ�ͼ�ε����ʿ�֪��FG=FG�䣬��Ϊ�ı���H H��G��GΪ�����Σ�����GH=GG��=2GF����FG=x����HG=2x���ɣ�1����֪��$\frac{AK}{AD}=\frac{GH}{CB}$���Ӷ�����ã�GF=$\frac{24}{7}$��GH=$\frac{48}{7}$��AK=$\frac{32}{7}$��Ȼ�����������ε������ʽ��⼴�ɣ�
����FG�ij�Ϊx����AK�ij�Ϊ��8-x��������á�AHG������͡�GCG���������Ӷ��ɵõ�y=$��\frac{8}{x}-1��^{2}+2$��Ȼ�����x��ȡֵ��Χ��3��x��5���y�����ֵ���ɣ�
��� �⣺��1����FG�ij�Ϊx����AK�ij�Ϊ��8-x����
���ı���EFGHΪ���Σ�
��HG��BC��
��$\frac{AK}{AD}=\frac{GH}{CB}$������$\frac{8-x}{8}=\frac{GH}{12}$��
��GH=$\frac{3}{2}��8-x��$��
����EFGH���=GH•GF=$\frac{3}{2}��8-x��x$=-$\frac{3}{2}{x}^{2}+12x$=-$\frac{3}{2}��x-4��^{2}+24$��
�൱x=4ʱ�����ε���������ֵ��
��GF=4��EF=GH=6��
��EF��GF=3��2��
��2������ͼ1��ʾ��
����Գ�ͼ�ε����ʿ�֪��FG=FG�䣬
���ı���H H��G��GΪ�����Σ�
��GH=GG��=2GF��
��FG=x����HG=2x.$\frac{8-x}{8}=\frac{2x}{12}$�ɣ�1����֪��$\frac{AK}{AD}=\frac{GH}{CB}$����$\frac{8-x}{8}=\frac{2x}{12}$
��ã�x=$\frac{24}{7}$��
��GF=$\frac{24}{7}$��GH=$\frac{48}{7}$��AK=$\frac{32}{7}$��
��AHG�����=$\frac{1}{2}GH•AK=\frac{1}{2}��\frac{48}{7}��\frac{32}{7}$=$\frac{768}{49}$��
����ͼ2��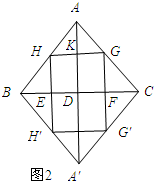
��FG�ij�Ϊx����AK�ij�Ϊ��8-x����
�ɣ�1����֪��GH=$\frac{3}{2}��8-x��$��
���AHG�����=$\frac{1}{2}GH•AK$=$\frac{3}{2}��8-x��^{2}$��
FC=$\frac{1}{2}$��BC-FE��=$\frac{1}{2}��BC-GH��$=$\frac{1}{2}[12-\frac{3}{2}��8-x��]$=$\frac{3}{4}x$
���GCG������=$\frac{1}{2}GG��•FC$=$\frac{1}{2}��2x��\frac{3}{2}x$=$\frac{3}{4}{x}^{2}$��
��y=$\frac{{S}_{1}}{{S}_{2}}+2$��
��y=$\frac{\frac{3}{2}��8-x��^{2}}{\frac{3}{4}{x}^{2}}+2$=$\frac{2����8-x��^{2}}{{x}^{2}}$=2$��\frac{8}{x}-1��^{2}+2$��
��3��x��5��
�൱x=3ʱ��y�����ֵ��
��y�����ֵ=2��$��\frac{8}{3}-1��^{2}+2$=$\frac{68}{9}$��
���� ���⿼��������������ε����ʡ����Ρ������Ρ����������ε����ʺͶ��κ������ۺ�Ӧ�ã��������������ε���������������߶εij��ȣ��ú�x��ʽ�ӱ�ʾ���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
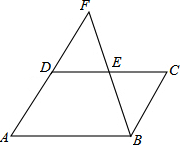 ��ͼ����E��ƽ���ı���ABCD�ı�CD���е㣬AD��BE���ӳ����ཻ�ڵ�F��DF=3��DE=2����ƽ���ı���ABCD���ܳ�Ϊ14��
��ͼ����E��ƽ���ı���ABCD�ı�CD���е㣬AD��BE���ӳ����ཻ�ڵ�F��DF=3��DE=2����ƽ���ı���ABCD���ܳ�Ϊ14���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڱ߳�Ϊ4��������ABCD�У�E��F�ֱ���CD��AD�ϵĵ㣬��CE=DF��BE��CF���ڵ�M��
��ͼ���ڱ߳�Ϊ4��������ABCD�У�E��F�ֱ���CD��AD�ϵĵ㣬��CE=DF��BE��CF���ڵ�M���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �˿���ͬ�ij����ε�שƴ��һ�����Σ���ÿ�鳤���ε�ש�ij��Ϳ��ֱ���45cm��15cm��
�˿���ͬ�ij����ε�שƴ��һ�����Σ���ÿ�鳤���ε�ש�ij��Ϳ��ֱ���45cm��15cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com