
 (2012•乌鲁木齐)如图是一个抛物线形拱桥的示意图,桥的跨度AB为100米,支撑桥的是一些等距的立柱,相邻立柱的水平距离为10米(不考虑立柱的粗细),其中距A点10米处的立柱FE的高度为3.6米.
(2012•乌鲁木齐)如图是一个抛物线形拱桥的示意图,桥的跨度AB为100米,支撑桥的是一些等距的立柱,相邻立柱的水平距离为10米(不考虑立柱的粗细),其中距A点10米处的立柱FE的高度为3.6米.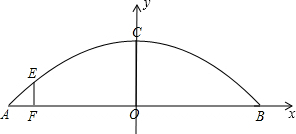
|
|
| 1 |
| 250 |
| 1 |
| 250 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
 (2012•乌鲁木齐)王老师将本班的“校园安全知识竞赛”成绩(成绩用s表示,满分为100分)分为5组,第1组:50≤x<60,第2组:60≤x<70,…,第5组:90≤x<100.并绘制了如图所示的频率分布表和频数分布直方图(不完整).
(2012•乌鲁木齐)王老师将本班的“校园安全知识竞赛”成绩(成绩用s表示,满分为100分)分为5组,第1组:50≤x<60,第2组:60≤x<70,…,第5组:90≤x<100.并绘制了如图所示的频率分布表和频数分布直方图(不完整).| 分组编号 | 成绩 | 频数 | 频率 |
| 第1组 | 50≤s<60 | 0.04 | |
| 第2组 | 60≤s<70 | 8 | 0.16 |
| 第3组 | 70≤s<80 | 0.4 | |
| 第4组 | 80≤s<90 | 17 | 0.34 |
| 第5组 | 90≤s≤100 | 3 | 0.06 |
| 合计 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com