
分析 如图,作出图形由勾股定理得到BD=$\sqrt{C{D}^{2}+B{C}^{2}}$=$\sqrt{8+4\sqrt{3}}$,根据三角函数的定义即可得到结论.
解答 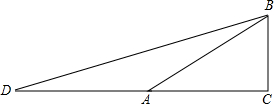 解:如图,作△ABC,使∠C=90°,∠A=30°,令AB=2,BC=1,AC=$\sqrt{3}$,延长CA至点D,使AD=AC,连接BD,则∠D=15°,
解:如图,作△ABC,使∠C=90°,∠A=30°,令AB=2,BC=1,AC=$\sqrt{3}$,延长CA至点D,使AD=AC,连接BD,则∠D=15°,
∵AD=AB=2,∴CD=2+$\sqrt{3}$,由勾股定理得:BD=$\sqrt{C{D}^{2}+B{C}^{2}}$=$\sqrt{8+4\sqrt{3}}$,
∴cos15°=$\frac{CD}{BD}$=$\frac{2+\sqrt{3}}{\sqrt{8+4\sqrt{3}}}$=$\frac{(2+\sqrt{3})(\sqrt{8+4\sqrt{3}})}{8+4\sqrt{3}}$=$\frac{\sqrt{6+2\sqrt{6}•\sqrt{2}+2}}{4}$=$\frac{\sqrt{(\sqrt{6}+\sqrt{2})^{2}}}{4}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$.
点评 本题考查了解直角三角形,正确的画出图形是解题的关键.


 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\frac{\sqrt{2}+1}{2}$ | C. | -1 | D. | $\frac{1-\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
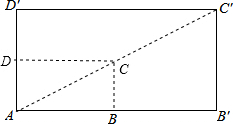 如图,矩形ABCD与矩形AB′C′D′是位似图形,已知矩形ABCD的周长是25cm,BB′=4cm,DD′=2cm,求矩形ABCD和AB′C′D′的面积比.
如图,矩形ABCD与矩形AB′C′D′是位似图形,已知矩形ABCD的周长是25cm,BB′=4cm,DD′=2cm,求矩形ABCD和AB′C′D′的面积比.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
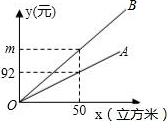 某市发改委举行居民用水价格调整听证会,届时将有两个方案提供听证.如图,射线OA、射线OB分别表示现行的、方案一的每户每月的水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;
某市发改委举行居民用水价格调整听证会,届时将有两个方案提供听证.如图,射线OA、射线OB分别表示现行的、方案一的每户每月的水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;| 阶数 | 用水量(立方米) | 用水价格(元/立方米) |
| 第一阶 | 0~15(含15)的部分 | 2.61 |
| 第二阶 | 15~25(含25)的部分 | 3.92 |
| 第三阶 | 25以上的得分 | n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com