
【题目】写出下列问题中的关系式,并指出其中的变量和常量.
(1)直角三角形中一个锐角a与另一个锐角β之间的关系;
(2)一盛满30吨水的水箱,每小时流出0.5吨水,试用流水时间t(小时)表示水箱中的剩水量y(吨).
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点△ABC(顶点是网格线的交点的三角形)的顶点A(-4,5),C(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系,并计算△ABC的面积;
(2)作出△ABC关于y轴对称的△A′B′C′;
(3)点P在x轴上,且△POB的面积等于△ABC面积的一半,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y= ![]() (k≠0)在第一象限的图象经过顶点A(m,m+3)和CD上的点E,且OB﹣CE=1.直线l过O、E两点,则tan∠EOC的值为( )
(k≠0)在第一象限的图象经过顶点A(m,m+3)和CD上的点E,且OB﹣CE=1.直线l过O、E两点,则tan∠EOC的值为( ) 
A.![]()
B.5
C.![]()
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示.

现有以下4个结论:
①快递车从甲地到乙地的速度为100千米/小时;
②甲、乙两地之间的距离为120千米;
③图中点B的坐标为(3.75,75);
④快递车从乙地返回时的速度为90千米/小时
以上结论正确的是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AD平分∠BAC,EM是AD的中垂线,交BC延长线于E. 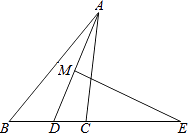
(1)连接AE,证明:∠EAC=∠B.
(2)求证:DE2=BECE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示. 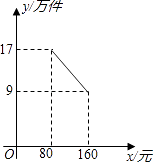
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?求出当盈利最大或亏损最小时的产品售价;
(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,公司第二年重新确定产品售价,能否使前两年盈利总额达790万元?若能,求出第二年产品售价;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
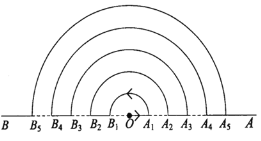
【题目】点O在直线AB上,点A1,A2,A3,……在射线OA上,点B1, B2,B3,……在射线OB上,图中的每一个实线段和虚线段的长均为1个单位长度.一个动点M从O点出发,以每秒1个单位长度
的速度按如图所示的箭头方向沿着实线段和以点O为圆心的半圆匀速运动,即从O![]() A1
A1![]() B1
B1![]() B2
B2![]() A2……按此规律,则动点M到达A10点处所需时间为 __________秒.(结果保留π)
A2……按此规律,则动点M到达A10点处所需时间为 __________秒.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的直角坐标系中,画出函数y=-2x+3的图象,并结合图象回答下列问题:
(1)y的值随x值的增大而 (填“增大”或“减小”);
(2)图象与x轴的交点坐标是 ;图象与y轴的交点坐标是 ;
(3)当x 时,y <0 ;
(4)直线y=-2x+3与两坐标轴所围成的三角形的面积是: .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com