
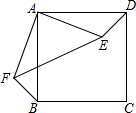
 如图,将正方形ABCD中的△ADE绕着点A顺时针旋转与△ABF重合,若AE=4,则EF的长为4$\sqrt{2}$.
如图,将正方形ABCD中的△ADE绕着点A顺时针旋转与△ABF重合,若AE=4,则EF的长为4$\sqrt{2}$.  小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
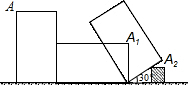 如图,小虎使一长为4cm,宽为2cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角.若连接AA2,则线段AA2的长(精确到0.1)约为( )
如图,小虎使一长为4cm,宽为2cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角.若连接AA2,则线段AA2的长(精确到0.1)约为( )| A. | 7.7cm | B. | 8.3cm | C. | 10.7cm | D. | 68.8cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com