
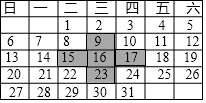
 在如图日历中,十字框框出了5个数.
在如图日历中,十字框框出了5个数.分析 (1)根据所给数据进行计算可得答案;
(2)根据图上的数之间的关系可得:中间一个为x,上面的数是x-1,下面的数是x+1,前面一个是x-7,后面一个是x+7,然后再计算这五个数的和即可;
(3)这个关系对任何一个月的日历都成立,理由为:日历都具有此规律.
解答 解:(1)9+15+16+17+23=80=16×5,
十字框中的5个数的和是十字框中间的数的5倍.
(2)成立.如图,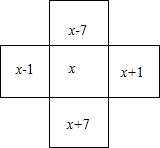
设十字框中的5个数分别是:上面的数是x-1,下面的数是x+1,前面一个是x-7,后面一个是x+7,
(x-1)+(x+1)+x+(x-7)+(x+7)=5x;
(3)这个关系对任何一个月的日历都成立,理由为任何一个日历表都具有这种排列规律.
点评 此题考查一元一次方程的实际运用,根据日历表中的数字排列规律解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=kx+3与x轴,y轴分别交于A,B两点,tan∠OAB=$\frac{3}{4}$,点C(x,y)是直线y=kx+3上与A,B不重合的动点.
如图,直线y=kx+3与x轴,y轴分别交于A,B两点,tan∠OAB=$\frac{3}{4}$,点C(x,y)是直线y=kx+3上与A,B不重合的动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com