练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．关于x的方程$\frac{4-ax}{x+2}$=3的解为非正数，则a的取值范围是（　　）
    A．a＞-3B．a≥-3C．a＞-3且a≠-2D．a＜-3

    分析 先解一元一次方程$\frac{4-ax}{x+2}$=3得到x=-$\frac{2}{3+a}$，利用解为非正数得到-$\frac{2}{a+3}$≤0，然后解此不等式即可．

    解答 解：解方程$\frac{4-ax}{x+2}$=3得x=-$\frac{2}{a+3}$，
    ∵关于x的方程$\frac{4-ax}{x+2}$=3的解为非正数，
    ∴-$\frac{2}{a+3}$＜0，
    解得：a＞-3且a≠-2．
    故选C．

    点评 此题考查了分式方程的解，以及解一元一次不等式，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．若以三个数为三角形三边的长能构成直角三角形，我们就把它们称为一组勾股数，如3，4，5，勾股数之间存在一种奇妙的联系，观察下表，结合表中数的规律及相关知识，求出b，c的值
    举例猜　　　想
    5、12、1352=12+13
    7、24、2572=24+25
    ……
    13、b、c132=b+c

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．若2m+3n=3，求4m•8n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．写出下列数的第n个数：
    （1）1，2，3，4，5，…n
         1，3，5，7，9…2n-1
         2，4，6，8，10…2n
    （2）2，4，8，16…2n
         3，9，27，81…3n
    （3）2，5，10，17…n2+1
         3，8，15，24…（n+1）2-1
         3，6，11，18…n2+2
         2，9，28，65…n3+1
    （4）5，8，11，14…3n+2
         7，12，17，22…5n+2
         10，17，24，31…7n+3
         3，7，11，15…4n-1
    （5）1，3，7，13…1+2+4+…+2n-1
         4，8，14，22…n2+n+2
         4，10，18，28…n2+3n．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图．在Rt△ABC中，∠C=90°，BC=$\sqrt{3}$，CD⊥AB，垂足为D，AD=2，求AB的长和tanA的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．寻求某些勾股数的规律：
    （1）对于任何一组已知的勾股数都扩大相同的正整数倍后，就得到了一组新的勾股数．例如：32+42=52，若把它扩大2倍、3倍，就分别得到62+82=102和92+122=152，…若把它扩大11倍，就得到332+442=552，若把它扩大n倍（n为正整数），就得到（3n）2+（4n）2=（5n）2．
     （2）对于任意一个大于1的奇数，存在着下列勾股数：
     若勾股数为3，4，5，因为32=52-42，则有32=4+5；
    若勾股数为5，12，13，则有52=12+13；
    若勾股数为7，24，25，则有72=24+25；…
    若勾股数为17，a，b（a＜b），根据以上的规律，求a、b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

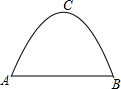    2．如图所示，某工厂大门是一抛物线形水泥建筑物，大门地面宽AB=4m，顶部C离地面高度为4m，现有一辆满载货物的汽车欲通过大门，货物顶部距离地面2m，装货宽度为2.5m，试判断这辆汽车能否顺利通过大门？通过计算说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知：如图，在△ABC中，AB=10，∠C=60°，求△ABC外接圆⊙O的半径r．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．定义新运算，对于任意实数a，b，都有a?b=a（a-b）+1，等式右边是通常的加法、减法及乘法运算．
    比如：2?5=2×（2-5）+1=2×（-3）+1=-6+1
    （1）求（-2）?3的值；
    （2）求$\sqrt{3}$?（-$\sqrt{2}$）的值．

    查看答案和解析>>

    同步练习册答案