练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．下面给出5个式子：①3x＞5；②x+1；③1-2y≤0；④x-2≠0；⑤3x-2=0．其中是不等式的个数有（　　）
    A．2个B．3个C．4个D．5个

    分析 不等式就是含有不等号，表示不等关系的式子，据此即可判断．

    解答 解：不等式有：：①3x＞5；③1-2y≤0；④x-2≠0共3个．
    故选B．

    点评 本题考查了不等式的定义，理解定义是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    5．如图，已知AE=CF，∠AFD=∠CEB，添加一个条件后，仍无法判定△ADF≌△CBE的是（　　）
    A．∠A=∠CB．AD=CBC．BE=DFD．AD∥BC

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列关于图形旋转的说法不正确的是（　　）
    A．对应点到旋转中心的距离相等
    B．对应点与旋转中心所连线段的夹角等于旋转角
    C．旋转前后的图形全等
    D．旋转后，图形的大小，形状与位置都发生了变化

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．直线l1：y=x+1与直线l2：y=mx+n的交点P的横坐标为1，则下列说法错误的是（　　）
    A．点P的坐标为（1，2）
    B．关于x、y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$
    C．直线l1中，y随x的增大而减小
    D．直线y=nx+m也经过点P

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，已知直线y=-x+3与x轴、y轴分别交于A，B两点，抛物线y=-x2+bx+c经过A，B两点，点P在线段OA上，从点O出发，向点A以1个单位/秒的速度匀速运动；同时，点Q在线段AB上，从点A出发，向点B以$\sqrt{2}$个单位/秒的速度匀速运动，连接PQ，设运动时间为t秒．
    （1）求抛物线的函数表达式；
    （2）当t为何值时，△APQ是直角三角形？
    （3）过点P作PE∥y轴，交AB于点E，过点Q作QF∥y轴，交抛物线于点F，连接EF，当EF∥PQ时，求点F的坐标；
    （4）设抛物线顶点为M，连接BP，BM，MQ，当△BOP与△MBQ相似时，直接写出t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

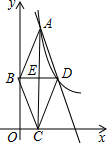    20．如图，点A是反比例函数y=$\frac{8}{x}$（x＞0）的图象上的一个动点，AC⊥x轴于点C；E是线段AC的中点，过点E作AC的垂线，与y轴和反比例函数的图象分别交于点B、D两点；连结AB、BC、CD、DA．设点A的横坐标为m．
    （1）求点D的坐标（用含有m的代数式表示）；
    （2）判断四边形ABCD的形状，并说明理由；
    （3）当m为何值时，四边形ABCD是正方形？并求出此时AD所在直线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．如图，直线l1：y=x-4与直线l2：y=-$\frac{4}{3}$x+3相交于点（3，-1），则方程组$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y}{2}=2}\\{x+\frac{3y}{4}=\frac{9}{4}}\end{array}\right.$的解是（　　）
    A．$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$B．$\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$C．$\left\{\begin{array}{l}{x=-1}\\{y=-3}\end{array}\right.$D．$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

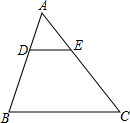    4．如图，在△ABC中，点D、E分别在边AB、AC上，AD：DB=2：3，∠B=∠ADE，则DE：BC等于（　　）
    A．1：2B．1：3C．2：3D．2：5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．下列命题：
    ①两直线平行，内错角相等；
    ②如果a＞0，b＞0，那么ab＞0；
    ③等边三角形是锐角三角形，
    其中原命题和它的逆命题都正确的有（　　）
    A．1个B．2个C．3个D．0个

    查看答案和解析>>

    同步练习册答案