练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AB和DE直立在地面上的两根立柱，已知AB=5m,某一时刻AB在太阳光下的影子长BC=3m．

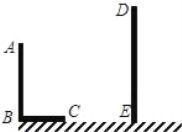
    （1）在图中画出此时DE在太阳光下的影子EF；

    （2）在测量AB影子长时，同时测量出EF=6m，计算DE的长．

    【答案】（1）详见解析；（2）10m

    【解析】

    （1）连接AC，过点D作DF∥AC，交直线BC于点F，线段EF即为DE的投影；

    （2）易证△ABC∽△DEF，再根据相似三角形的对应边成比例进行解答即可.

    （1）连接AC，过点D作DF∥AC，交直线BC于点F，线段EF即为DE的投影．

    （2）∵AC∥DF，

    ∴∠ACB=∠DFE，

    ∵∠ABC=∠DEF=90°，

    ∴△ABC∽△DEF，

    ∴AB：DE=BC：EF，

    ∵AB=5m，BC=3m，EF=6m，

    ∴5：DE=3：6，

    ∴DE=10m．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知一个二次数图象上部分点的横坐标与纵坐标的对应值如下表所示：

    (1)求这个二次函数的达式；

    (2)在给定的平面直角坐标系中画出这个二次函数的图象；

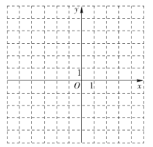
    (3)当时，直接写出的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读资料：我们把顶点在圆上，并且一边和圆相交、另一边和圆相切的角叫做弦切角，如下左图∠ABC所示。

    同学们研究发现：P为圆上任意一点，当弦AC经过圆心O时，且AB切⊙O于点A，此时弦切角∠CAB=∠P（图甲）

    证明：∵AB切⊙O于点A， ∴∠CAB=90°， 又∵AC是直径， ∴∠P=90° ∴∠CAB=∠P

    问题拓展：若AC不经过圆心O（如图乙），该结论:弦切角∠CAB=∠P还成立吗？

    请说明理由。

    知识运用：如图，AD是△ABC中∠BAC的平分线，经过点A的⊙O与BC切于点D，与AB、AC分别相交于E、F。 求证：EF∥BC。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD内接于⊙O，AB=AD，对角线BD为⊙O的直径，AC与BD交于点E．点F为CD延长线上，且DF=BC.

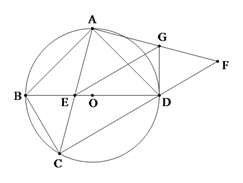
    （1）证明：AC=AF；

    （2）若AD=2，AF=，求AE的长；

    （3）若EG∥CF交AF于点G，连接DG.证明：DG为⊙O的切线.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形网格中，△ABC和△DEF相似，则关于位似中心与相似比叙述正确的是（　　）

    A. 位似中心是点B，相似比是2：1 B. 位似中心是点D，相似比是2：1

    C. 位似中心在点G，H之间，相似比为2：1 D. 位似中心在点G，H之间，相似比为1：2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，抛物线y=(x-2)2与x轴交于点A，与y轴交于点B，过点B作BC∥x轴，交抛物线于点C，过点A作AD∥y轴，交BC于点D，点P在BC下方的抛物线上(不与点B，C重合)，连接PC，PD，设△PCD的面积为S，则S的最大值是________。

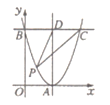
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1是实验室中的一种摆动装置，在地面上，支架是底边为的等腰直角三角形，摆动臂长可绕点旋转，摆动臂可绕点旋转，，.

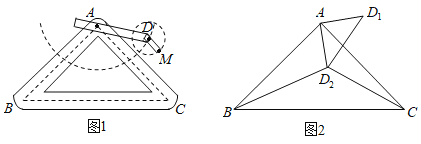
    （1）在旋转过程中：

    ①当三点在同一直线上时，求的长；

    ②当三点在同一直角三角形的顶点时，求的长.

    （2）若摆动臂顺时针旋转，点的位置由外的点转到其内的点处，连结，如图2，此时，，求的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是甲、乙两校男、女生人数的统计图．

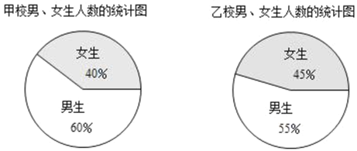
    根据统计图回答问题：

    （1）若甲校男生人数为273人，求该校女生人数；

    （2）方方同学说：“因为甲校女生人数占全校人数的40%，而乙校女生人数占全校人数的55%，所以甲校的女生人数比乙校女生人数少”，你认为方方同学说的对吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知点A（―3，6）、B（―9，一3），以原点O为位似中心，相似比为，把△ABO缩小，则点A的对应点A′的坐标是（ ）

    A．（―1，2）

    B．（―9，18）

    C．（―9，18）或（9，―18）

    D．（―1，2）或（1，―2）

    查看答案和解析>>

    同步练习册答案