
分析 (1)设甲内存卡每个x元,乙内存卡每个y元,依据“买2个甲内存卡和1个乙内存卡共用了90元,买了3个甲内存卡和2个乙内存卡用了160元”列出方程组并解答;
(2)设小亮准备购买A甲内存卡a个,则购买乙内存卡(10-a)个,根据关系式列出一元一次不等式方程组.求解再比较两种方案.
(3)设老板一上午卖了c个甲内存卡,d个乙内存卡,根据“甲内存卡每个赚10元,乙内存卡每个赚15元,一上午售出的内存卡共赚了100元”列出方程组,并解答.
解答 解:(1)设甲内存卡每个x元,乙内存卡每个y元,则
$\left\{\begin{array}{l}{2x+y=90}\\{3x+2y=160}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=20}\\{y=50}\end{array}\right.$.
答:甲内存卡每个20元,乙内存卡每个50元;
(2)设小亮准备购买A甲内存卡a个,则购买乙内存卡(10-a)个,则
$\left\{\begin{array}{l}{20a+50(10-a)≥300}\\{20a+50(10-a)≤350}\end{array}\right.$
解得5≤a≤6$\frac{2}{3}$
根据题意,a的值应为整数,所以a=5或a=6.
方案一:当a=5时,购买费用为20×5+50×(10-5)=350元;
方案二:当a=6时,购买费用为20×6+50×(10-6)=320元;
∵350>320
∴购买A商品6件,B商品4件的费用最低.
答:有两种购买方案,方案一:购买A商品5件,B商品5件;方案二:购买A商品6件,B商品4件,其中方案二费用最低.
(3)设老板一上午卖了c个甲内存卡,d个乙内存卡,则
10c+15d=100.
整理,得
2c+3d=20.
∵c、d都是正整数,
∴当c=10时,d=0;
当c=7时,d=2;
当c=4时,d=4;
当c=1时,d=6.
综上所述,共有4种销售方案:
方案一:卖了甲内存卡10个,乙内存卡0个;
方案二:卖了甲内存卡7个,乙内存卡2个;
方案三:卖了甲内存卡4个,乙内存卡4个;
方案四:卖了甲内存卡1个,乙内存卡6个.
点评 此题主要考查二元一次方程组及一元一次不等式方程组的应用,解决问题的关键是读懂题意,找到关键描述语,找到所求的量的大小关系.


科目:初中数学 来源: 题型:解答题
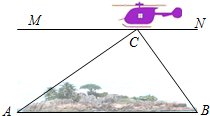 如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A、B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A、B的距离.
如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A、B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A、B的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.9×1013 | B. | 4.0×1013 | C. | 3.97×105 | D. | 3.98×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2015 | B. | -2015 | C. | $\frac{1}{2015}$ | D. | -$\frac{1}{2015}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com