
 如图所示,某地新建一座石拱桥,桥拱是圆弧形,它的跨度(弧所对的弦的长)为40m,拱高(弧的中点到弦的距离)为8m,求桥拱得半径R.
如图所示,某地新建一座石拱桥,桥拱是圆弧形,它的跨度(弧所对的弦的长)为40m,拱高(弧的中点到弦的距离)为8m,求桥拱得半径R.科目:初中数学 来源: 题型:
 (黑线表示被弟弟涂掉的部分),请你将这道作业题补充完整,并列方程解答.
(黑线表示被弟弟涂掉的部分),请你将这道作业题补充完整,并列方程解答.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
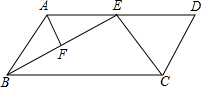 如图,AB∥CD,BC∥AD,BE、CE分别是∠ABC、∠BCD的平分线,F是BE的中点.
如图,AB∥CD,BC∥AD,BE、CE分别是∠ABC、∠BCD的平分线,F是BE的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com