
【题目】(1)解方程:![]() ;
;
(2)如图,在平面直角坐标系中,![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() 、
、![]() 、
、![]() .
.
①将![]() 向左平移5个单位得到
向左平移5个单位得到![]() ,写出
,写出![]() 三顶点的坐标;
三顶点的坐标;
②将![]() 绕原点
绕原点![]() 逆时针旋转
逆时针旋转![]() 后得到
后得到![]() ,请你画出
,请你画出![]() ;
;
③![]() 与
与![]() 重合部分的面积为 .(直接写出)
重合部分的面积为 .(直接写出)
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ,
,![]() ,
,![]() ;②见解析;③
;②见解析;③![]()
【解析】
(1)利用因式分解法解一元二次方程即可;
(2)①将![]() 向左平移5个单位得到
向左平移5个单位得到![]() ,根据点的平移规律:左减右加、上加下减,即可得出结论;
,根据点的平移规律:左减右加、上加下减,即可得出结论;
②将![]() 绕原点
绕原点![]() 逆时针旋转
逆时针旋转![]() 后得到
后得到![]() 即可;
即可;
③设A1C1与A2C2交于点D,找出![]() 与
与![]() 重合部分△A2C1D,然后证出△A1A2C1是直角三角形,并求出其面积,然后证出
重合部分△A2C1D,然后证出△A1A2C1是直角三角形,并求出其面积,然后证出![]() ⊥
⊥![]() ,根据三线合一和三角形中线的性质即可求出结论.
,根据三线合一和三角形中线的性质即可求出结论.
(1)解:![]() ,
,
∴![]() ,
,
∴![]() ,
,![]()
(2)①将![]() 向左平移5个单位得到
向左平移5个单位得到![]() ,如图所示,
,如图所示,![]() 即为所求
即为所求
∵![]() 、
、![]() 、
、![]()
∴![]() ,
,![]() ,
,![]()
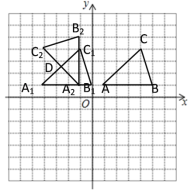
②将![]() 绕原点
绕原点![]() 逆时针旋转
逆时针旋转![]() 后得到
后得到![]() ,如图所示,
,如图所示,![]() 即为所求;
即为所求;
③设A1C1与A2C2交于点D,
由平面直角坐标系可知:A2的坐标为(-1,1),![]() 与
与![]() 重合部分为△A2C1D
重合部分为△A2C1D
∴A2C1 =A1A2=3,且∠A1A2 C1=90°
∴△A1A2C1是直角三角形,
∴S△A1A2C1=![]() A2C1·A1A2=
A2C1·A1A2=![]()
∵![]() 是由AC平移得到,
是由AC平移得到,![]() 是由AC绕原点逆时针旋转90°得到
是由AC绕原点逆时针旋转90°得到
∴![]() ∥AC,
∥AC,![]() ⊥AC
⊥AC
∴![]() ⊥
⊥![]()
∴点D为A1C1的中点
∴S△A2C1D=![]() S△A1A2C1=
S△A1A2C1=![]()


科目:初中数学 来源: 题型:
【题目】某企业在甲地又一工厂(简称甲厂)生产某产品,2017年的年产量过百万,2018年甲厂经过技术改造,日均生产的该产品数是该厂2017年的2倍还多2件.
(1)若甲厂2018年生产200件该产品所需的时间与2017年生产98件该产品所需的时间相同,则2017年甲厂日均生产该产品多少件?
(2)由于该产品深受顾客喜欢,2019年该企业在乙地建立新厂(简称乙厂)生产该产品,乙厂的日均生产的该产品数是甲厂2017年的3倍还要多5件,同年该企业要求甲、乙两厂分别生产m,n件产品(甲厂的日均产量与2018年相同),m:n=14:25,若甲、乙两厂同时开始生产,谁先完成任务?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
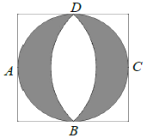
【题目】文艺复兴时期,意大利艺术大师达芬奇曾研究过圆弧所围成的许多图形的面积问题. 如图所示称为达芬奇的“猫眼”,可看成圆与正方形的各边均相切,切点分别为![]() ,
,![]() 所在圆的圆心为点
所在圆的圆心为点![]() (或
(或![]() ). 若正方形的边长为2,则图中阴影部分的面积为( )
). 若正方形的边长为2,则图中阴影部分的面积为( )
A. ![]() B. 2C.
B. 2C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有四张完全相同的不透明卡片,其正面分别写有数字-2,-1,0,2,把这四张卡片背面朝上洗匀后放在桌面上.
(1)随机抽取一张卡片,求抽取的卡片上的数字为负数的概率;
(2)先随机抽取卡片,其上的数字作为点A的横坐标;然后放回并洗匀,再随机抽取一张卡片,其上的数字作为点A的纵坐标,试用画树状图或列表的方法求出点A在直线y=2x上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的网格中,每个格子都是边长为1的小正方形,已知△ABC三个顶点的坐标分别为A(1,1).B(4,2)、C(3,4).
(1)请画出将△ABC绕点A顺时针旋转90°后得到的△AB1C1;
(2)请画出△ABC关于原点O成中心对称的△A2B2C2;
(3)当△ABC绕点A顺时针旋转90°后得到△AB1C1,求点C所经过的路径长.
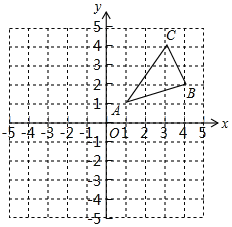
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,A的坐标为(0,0),B的坐标为(﹣3,1).
(1)将线段AB绕点A逆时钟旋转θ度(0<θ<180),得到对应的线段AE,当AE∥CD时,设在此过程中线段AB所扫过的区域面积为S,点B所经过的路径长为l,则S= ;l= .
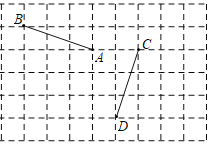
(2)是否存在点P,使得线段AB可由线段CD绕点P旋转一个角度而得到?若存在,直接写出点P的坐标(写出一个即可);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
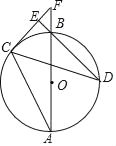
【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD,过点C作CE⊥DB,垂足为E,直径AB与CE的延长线相交于F点.
(1)求证:CF是⊙O的切线;
(2)当BD=![]() ,sinF=
,sinF=![]() 时,求OF的长.
时,求OF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com