
【题目】如图,二次函数![]() 图象的顶点为
图象的顶点为![]() ,其图象与
,其图象与![]() 轴的交点
轴的交点![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() ,
,![]() .与
.与![]() 轴负半轴交于点
轴负半轴交于点![]() ,在下面五个结论中:
,在下面五个结论中:
①![]() ;②
;②![]() ;③
;③![]() ;④只有当
;④只有当![]() 时,
时,![]() 是等腰直角三角形;⑤使
是等腰直角三角形;⑤使![]() 为等腰三角形的
为等腰三角形的![]() 值可以有四个.
值可以有四个.
其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
【答案】A
【解析】
先根据图象与x轴的交点A,B的横坐标分别为-1,3确定出AB的长及对称轴,再由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
①∵图象与x轴的交点A,B的横坐标分别为-1,3,
∴AB=4,
∴对称轴x=-![]() =1,
=1,
即2a+b=0.
故①错误;
②根据图示知,当x=1时,y<0,即a+b+c<0.
故②错误;
③∵A点坐标为(-1,0),
∴a-b+c=0,而b=-2a,
∴a+2a+c=0,即c=-3a.
故③正确;
④当a=![]() ,则b=-1,c=-
,则b=-1,c=-![]() ,对称轴x=1与x轴的交点为E,如图,
,对称轴x=1与x轴的交点为E,如图,
∴抛物线的解析式为y=![]() x2-x-
x2-x-![]() ,
,
把x=1代入得y=![]() -1-
-1-![]() =-2,
=-2,
∴D点坐标为(1,-2),
∴AE=2,BE=2,DE=2,
∴△ADE和△BDE都为等腰直角三角形,
∴△ADB为等腰直角三角形.
故④正确;
⑤要使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,
当AB=BC=4时,
∵AO=1,△BOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16-9=7,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=-![]() ,
,
与2a+b=0、a-b+c=0联立组成解方程组,解得a=![]() ;
;
同理当AB=AC=4时
∵AO=1,△AOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16-1=15,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=-![]()
与2a+b=0、a-b+c=0联立组成解方程组,解得a=![]() ;
;
同理当AC=BC时
在△AOC中,AC2=1+c2,
在△BOC中BC2=c2+9,
∵AC=BC,
∴1+c2=c2+9,此方程无解.
经解方程组可知只有两个a值满足条件.
故⑤错误.
综上所述,正确的结论是③④.
故选A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在第一象限内作射线OC,与x轴的夹角为30°,在射线OC上取点A,过点A作AH⊥x轴于点H.在抛物线y=x2(x>0)上取点P,在y轴上取点Q,使得以P、O、Q为顶点,且以点Q为直角顶点的三角形与△AOH全等,则符合条件的点A的坐标是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明家小区空地上有两棵笔直的树![]() 、
、![]() .一天,他在
.一天,他在![]() 处测得树顶
处测得树顶![]() 的仰角
的仰角![]() ,在
,在![]() 处测得树顶
处测得树顶![]() 的仰角
的仰角![]() ,线段
,线段![]() 恰好经过树顶
恰好经过树顶![]() .已知
.已知![]() 、
、![]() 两处的距离为
两处的距离为![]() 米,两棵树之间的距离
米,两棵树之间的距离![]() 米,
米,![]() 、
、![]() 、
、![]() 、
、![]() 四点.在一条直线上,求树
四点.在一条直线上,求树![]() 的高度.(结果精确到
的高度.(结果精确到![]() 米,参考数据:
米,参考数据:![]() ,
,![]() ,
,![]() .)
.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,且CF⊥AD于H,下列判断,①BG是△ABD中边AD上的中线;②AD既是△ABC中∠BAC的角平分线,也是△ABE中∠BAE的角平分线;③CH既是△ACD中AD边上的高线,也是△ACH中AH边上的高线,其中正确的个数是( )
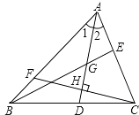
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,在ABCD中,点E是AB中点,连接DE并延长,交CB的延长线于点F.
(1)求证:△ADE≌△BFE;
(2)如图2,点G是边BC上任意一点(点G不与点B、C重合),连接AG交DF于点H,连接HC,过点A作AK∥HC,交DF于点K.
①求证:HC=2AK;
②当点G是边BC中点时,恰有HD=nHK(n为正整数),求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,
的图象如图所示,
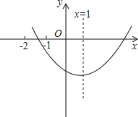
![]() 给出三个结论:①
给出三个结论:①![]() ;②
;②![]() ;③
;③![]() ,其中正确结论的序号是:________.
,其中正确结论的序号是:________.
![]() 给出三个结论:①
给出三个结论:①![]() ;②
;②![]() ;③
;③![]() ,其中正确结论的序号是:________.
,其中正确结论的序号是:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 交抛物线的对称轴于点
交抛物线的对称轴于点![]() ,
,![]() 是抛物线的顶点.
是抛物线的顶点.
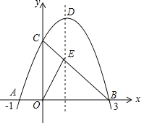
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 直接写出点
直接写出点![]() 和点
和点![]() 的坐标;
的坐标;
![]() 若点
若点![]() 在第一象限内的抛物线上,且
在第一象限内的抛物线上,且![]() ,求
,求![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在要从甲、乙两名学生中选择一名学生去参加比赛,因甲乙两人的5次测试总成绩相同,所以根据他们的成绩绘制了尚不完整的统计图表进行分析.
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 90 | 70 | 80 | 100 | 60 |
乙成绩 | 70 | 90 | 90 | a | 70 |
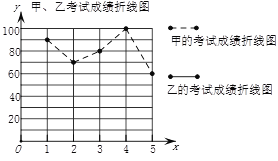
请同学们完成下列问题:
(1)a=________,![]() =________;
=________;
(2)请在图中完成表示乙成绩变化情况的折线:
(3)S2甲=200,请你计算乙的方差;
(4)可看出________将被选中参加比赛.(第1问和第4问答案可直接填写在答题卡的横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,D在边AC上,且
,D在边AC上,且![]() .
.
![]() 如图1,填空
如图1,填空![]() ______
______![]() ,
,![]() ______
______![]()
![]() 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线![]() 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E.
![]() 求证:
求证:![]() 是等腰三角形;
是等腰三角形;
![]() 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com