
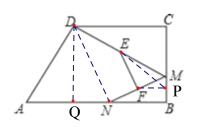
【题目】如图,在四边形ABCD中,AB∥CD,∠C=90°,AB=8,AD=CD=5,点M为BC上异于B、C的一定点,点N为AB上的一动点,E、F分别为DM、MN的中点,当N从A到B的运动过程中,线段EF扫过图形的面积为 ( )

A.4B.4.5C.5D.6
【答案】A
【解析】
取MB的中点P,连接FP,EP,DN,由中位线的性质,可得当N从A到B的运动过程中,点F在FP所在的直线上运动,即:线段EF扫过图形为EFP,求出当点N与点A重合时,FP的值,以及FP上的高,进而即可求解.
取MB的中点P,连接FP,EP,DN,
∵FP是MNB的中位线,EF是DMN的中位线,
∴FP∥BN,FP=![]() ,EF∥DN,EF=
,EF∥DN,EF=![]() ,
,
∴当N从A到B的运动过程中,点F在FP所在的直线上运动,即:线段EF扫过图形为EFP.
∴当点N与点A重合时,FP=![]() =
=![]() =4,
=4,
过点D作DQ⊥AB于点Q,
∵AB∥CD,∠C=90°,AB=8,AD=CD=5,
∴AQ=8-5=3,
∴DQ=![]() ,
,
∴当点N与点Q重合时,EF=![]() ,EF∥DQ,即:EF⊥AB,即:EF⊥FP,
,EF∥DQ,即:EF⊥AB,即:EF⊥FP,
∴EFP中,FP上的高=2,
∴当N从A到B的运动过程中,线段EF扫过图形的面积=![]() ×4×2=4.
×4×2=4.
故选A.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
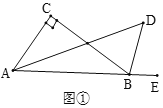
【题目】(1)如图①,在△ABC中,∠C=90°,∠BAC的平分线与外角∠CBE的平分线相交于点D,求∠D的度数.
(2)如图②,将(1)中的条件“![]() ”改为
”改为![]() ,其它条件不变,请直接写出
,其它条件不变,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的发展,智能制造逐渐成为一种可能的生产方式.重庆某电子零部件生产商原来采用自动化程度较低的传统生产方式,工厂有熟练工人和新工人共100人,熟练工平均每天能生产30个零件,新工人平均每天能生产20个零件,所有工人刚好用30天完成了一项7.2万个零件的生产任务.
(1)请问该工厂有熟练工,新工人各多少人?(请列二元一次方程组解题)
(2)今年,某自动化技术团队为工厂提供了A、B两种不同型号的机器人,且两种机器人都可以单独完成零件的生产.已知A型机器人的售价为80万元/台,B型机器人的售价为120万元/台.工厂准备采购价值840万元的机器人设备,两种机器人都至少购买一台,若840万元刚好用完,求出所有可能的购买方案.
(3)已知一个零件的毛利润(只扣除了原材料成本)为10元,若选择传统生产方式,熟练工每月基本工资3000元,新工人每月基本工资2000元,在基本工资之上,工厂还需额外支付计件工资5元/件,传统生产方式的设备成本忽略不计.若选择智能制造方式生产,A型机器人每月生产零件1.5万个,B型机器人每月能生产零件2.7万个,1台A型机器人需要8名技术人员操控,一台B型机器人需要12名技术人员操控,技术人员每人工资1万元,实际生产过程中,一台A型机器人平均每月的总成本为6万元(包含所有设备成本和维护成本),一台B型机器人平均每月的总成本为8万元(包含所有设备成本和维护成本).请你比较传统的生产方式和(2)中的所有购买方案对应的智能生产方式,哪种生产方式每月的总利润最大,最大利润为多少万元?(注:每月均按30天计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年3月全国两会胜利召开,某学校就两会期间出现频率最高的热词:A.蓝天保卫战,B.不动产保护,C.经济增速,D.简政放权等进行了抽样调查,每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)从该校学生中随机抽取一个最关注热词D的学生的概率是多少?

【答案】(1)300;(2)60,90;(3)从该校学生中随机抽取一个最关注热词D的学生的概率是![]() .
.
【解析】试题分析:(1)根据A的人数为105人,所占的百分比为35%,求出总人数,即可解答;
(2)C所对应的人数为:总人数×30%,B所对应的人数为:总人数﹣A所对应的人数﹣C所对应的人数﹣D所对应的人数,即可解答;
(3)根据概率公式,即可解答.
试题解析:(1)105÷35%=300(人),
故答案为:300;
(2)n=300×30%=90(人),
m=300﹣105﹣90﹣45=60(人).
故答案为:60,90;
(3)从该校学生中随机抽取一个最关注热词D的学生的概率是![]() =
=![]() ,
,
答:从该校学生中随机抽取一个最关注热词D的学生的概率是![]() .
.
【题型】解答题
【结束】
26
【题目】已知正方形ABCD的边长为8,点E为BC的中点,连接AE,并延长交射线DC于点F,将△ABE沿着直线AE翻折,点B落在B′处,延长AB′,交直线CD于点M.
(1)判断△AMF的形状并证明;
(2)将正方形变为矩形ABCD,且AB=6,BC=8,若B′恰好落在对角线AC上时,得到图2,此时CF=_____, ![]() =_____;
=_____;
(3)在(2)的条件下,点E在BC边上.设BE为x,△ABE沿直线AE翻折后与矩形ABCD重合的面积为y,求y与x之间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,![]() ,
,![]() ,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小;
(3)求CQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-2x-3.
(1)求函数图象的顶点坐标,与x轴和y轴的交点坐标,并画出函数的大致图象;
(2)根据图象直接回答:当x满足 时,y<0;当-1<x<2时,y的范围是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AC是⊙O的直径,过点B作BE⊥AD,垂足为点E,AB平分∠CAE.
(1)判断BE与⊙O的位置关系,并说明理由;
(2)若∠ACB=30°,⊙O的半径为4,请求出图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
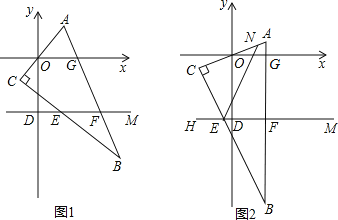
【题目】在平面直角坐标系中,D(0,-3),M(4,-3),直角三角形ABC的边与x轴分别交于O、G两点,与直线DM分别交于E、F点.
(1)将直角三角形ABC如图1位置摆放,请写出∠CEF与∠AOG之间的等量关系:______.
(2)将直角三角形ABC如图2位置摆放,N为AC上一点,∠NED+∠CEF=180°,请写出∠NEF与∠AOG之间的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
(1)请直接写出点A关于原点O对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com