
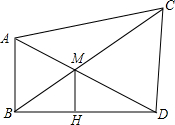
 如图,AB和CD表示两根直立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M,已知AB=10m,CD=15m,求点M离地面的高度MH.
如图,AB和CD表示两根直立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M,已知AB=10m,CD=15m,求点M离地面的高度MH. 分析 根据已知易得△ABM∽△DCM,可得对应高BH与HD之比,易得MH∥AB,可得△MDH∽△ADB,利用对应边成比例可得比例式,把相关数值代入求解即可.
解答 解:∵AB∥CD,
∴△ABM∽△DCM,
∴$\frac{BH}{HD}$=$\frac{AB}{CD}$=$\frac{10}{15}$=$\frac{2}{3}$,(相似三角形对应高的比等于相似比),
∵MH∥AB,
∴△MDH∽△ADB,
∴$\frac{MH}{AB}$=$\frac{DH}{BD}$=$\frac{3}{5}$,
∴$\frac{MH}{10}$=$\frac{3}{5}$,
解得MH=6.
答:点M离地面的高度MH为6m.
点评 此题主要考查了相似三角形的应用;用到的知识点为:平行于三角形一边的直线与三角形另两边相交,截得的两三角形相似;相似三角形的对应边成比例;对应高的比等于相似比;解决本题的突破点是得到BH与HD的比.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在Rt△ACB中,∠ACB=90°,M为AB上一点,且MB=MC,求证:MA=MC.
如图所示,在Rt△ACB中,∠ACB=90°,M为AB上一点,且MB=MC,求证:MA=MC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{81}$=±9 | B. | (-$\frac{1}{3}$)2=$\frac{1}{9}$ | C. | $\sqrt{12}$=2$\sqrt{3}$ | D. | |$\sqrt{3}$-2|=2-$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com