
 在小孔成像问题中,如图所示,若为O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物体AB长的( )
在小孔成像问题中,如图所示,若为O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物体AB长的( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2倍 | D. | 3倍 |
分析 如图,作OE⊥AB于E,EO的延长线交CD于F.由△AOB∽△DOC,推出$\frac{CD}{AB}$=$\frac{OF}{OE}$=$\frac{6}{18}$=$\frac{1}{3}$(相似三角形的对应高的比等于相似比),由此即可解决问题.
解答 解:如图,作OE⊥AB于E,EO的延长线交CD于F.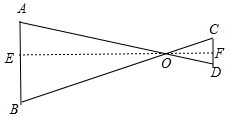
∵AB∥CD,
∴FO⊥CD,△AOB∽△DOC,
∴$\frac{CD}{AB}$=$\frac{OF}{OE}$=$\frac{6}{18}$=$\frac{1}{3}$(相似三角形的对应高的比等于相似比),
∴CD=$\frac{1}{3}$AB,
故选A.
点评 本题考查相似三角形的判定和性质,解题的关键是灵活运用所学知识解决问题,记住相似三角形对应高的比等于相似比,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
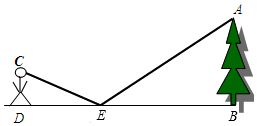 为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子水平放置在离B(树底)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,求树AB的高度.
为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子水平放置在离B(树底)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,求树AB的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com