
【题目】定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.如图1,∠ABC=∠ADC=90°,四边形ABCD是损矩形,则该损矩形的直径是线段AC.同时我们还发现损矩形中有公共边的两个三角形角的特点:在公共边的同侧的两个角是相等的.如图1中:△ABC和△ABD有公共边AB,在AB同侧有∠ADB和∠ACB,此时∠ADB=∠ACB;再比如△ABC和△BCD有公共边BC,在CB同侧有∠BAC和∠BDC,此时∠BAC=∠BDC.
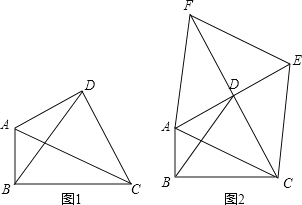
(1)请在图1中再找出一对这样的角来: = .
(2)如图2,△ABC中,∠ABC=90°,以AC为一边向外作菱形ACEF,D为菱形ACEF对角线的交点,连接BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由.
(3)在第(2)题的条件下,若此时AB=6,BD=8![]() ,求BC的长.
,求BC的长.
【答案】(1)∠ABD=∠ACD(或∠DAC=∠DBC );(2)四边形ACEF为正方形,理由见解析;(3)10
【解析】
(1)根据题意给出的性质即可得出一组角相等;
(2)先证明四边形ACEF为菱形,再证明四边形ABCD为损矩形,根据损矩形的性质即可求出四边形ACEF是正方形;
(3)过点D作DM⊥BC,过点E作EN⊥BC交BC的延长线于点N,可得△BDM为等腰直角三角形,从而得出△ABC≌△CNE根据性质即可得出BC的长.
(1)由图1得:△ABD和△ADC有公共边AD,在AD同侧有∠ABD和∠ACD,此时∠ABD=∠ACD;

故答案为:∠ABD=∠ACD(或∠DAC=∠DBC );
(2)四边形ACEF为正方形
证明:∵∠ABC=90°,BD平分∠ABC,
∴∠ABD=∠CBD=45°,
∵四边形ACEF为菱形,
∴AE⊥CF,即∠ADC=90°,
∵∠ABC=90°,
∴四边形ABCD为损矩形,
由(1)得∠ACD=∠ABD=45°,
∴∠ACE=2∠ACD=90°,
∴四边形ACEF为正方形.
(3)过点D作DM⊥BC,过点E作EN⊥BC交BC的延长线于点N,

∵∠DBM=45°,
∴△BDM为等腰直角三角形,
∴BM=DM=![]() ,
,
∵AC=EC,∠ACE=90°,∠ABC=CNE=90°,
∴∠ACB=∠CEN,
∴△ABC≌△CNE(AAS),
∴CN=AB=6,
∵DM∥EN,AD=DE,
∴BM=MN=8,
∴BC=BN﹣CN=2BM﹣CN=10.


科目:初中数学 来源: 题型:
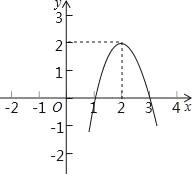
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2-![]() x+c交x轴于点A和点B(点A在原点的左侧,点B在原点的右侧),点A的坐标为(-3,0),点B的坐标为(1,0),交y轴于点C.
x+c交x轴于点A和点B(点A在原点的左侧,点B在原点的右侧),点A的坐标为(-3,0),点B的坐标为(1,0),交y轴于点C.
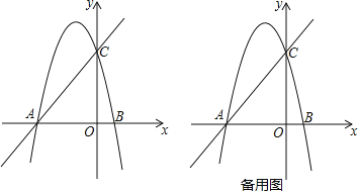
(1)求该抛物线的解析式;
(2)已知点P为抛物线上一点,直线PC与x轴交于点Q,使得PQ=![]() CQ,求P点坐标;
CQ,求P点坐标;
(3)若点M是抛物线对称轴上一点,点N是平面内一点,是否存在以A,C,M,N为顶点的矩形?若存在,请直接写出N点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=12,P是AB上一点,将△PBC沿直线PC折叠,顶点B的对应点是G,过点B作BE⊥CG,垂足为E,且在AD上,BE交PC于点F,则下列结论,其中正确的结论有( )
①BP=BF;②若点E是AD的中点,那么△AEB≌△DEC;③当AD=25,且AE<DE时,则DE=16;④在③的条件下,可得sin∠PCB=![]() ;⑤当BP=9时,BEEF=108.
;⑤当BP=9时,BEEF=108.
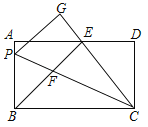
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
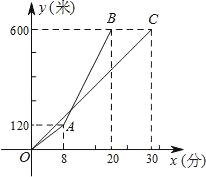
【题目】甲、乙两人沿同一路线登山,图中线段OC、折线OAB分别是甲、乙两人登山的路程y(米)与登山时间x(分)之间的函数图象.请根据图象所提供的信息,解答如下问题:
(1)求甲登山的路程与登山时间之间的函数关系式,并写出自变量x的取值范围;
(2)求乙出发后多长时间追上甲?此时乙所走的路程是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天府新区某校数学活动小组在一次活动中,对一个数学问题作如下探究:
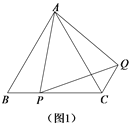
(1)问题发现:如图1,在等边△ABC中,点P是边BC上任意一点,连接AP,以AP为边作等边△APQ,连接CQ.求证:BP CQ;
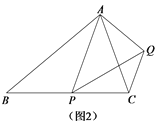
(2)变式探究:如图2,在等腰△ABC中,ABBC,点P是边BC上任意一点,以AP为腰作等腰△APQ,使AP PQ,APQ ABC,连接CQ.判断∠ABC和∠ACQ的数量关系,并说明理由;
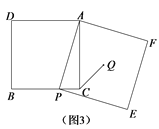
(3)解决问题:如图3,在正方形ADBC中,点P是边BC上一点,以AP为边作正方形 APEF,Q是正方形APEF的中心,连接CQ.若正方形APEF的边长为6,![]() ,求正方形ADBC的边长.
,求正方形ADBC的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程(请选择合适的方法)
(1)x2+4x=0;
(2)x2+![]() x﹣
x﹣![]() =0
=0
(3)3x(x﹣1)=4(x﹣1);
(4)x2﹣4x+4=(3﹣2x)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com