
| 成本价(万元/辆) | 售价(万元/辆) | |
| A型 | 30 | 32 |
| B型 | 42 | 45 |
分析 (1)根据已知信息和若经营者的购买资金不少于576万元且不多于600万元,列出不等式组,求解得出进车方案.
(2)根据已知列出利润函数式,求最值,选择方案.
(3)根据已知通过计算分析得出答案.
解答 解:(1)设A型汽车购进x辆,则B型汽车购进(16-x)辆.
根据题意得:$\left\{\begin{array}{l}{30x+42(16-x)≤600}\\{30x+42(16-x)≥576}\end{array}\right.$,
解得:6≤x≤8.
∵x为整数,
∴x取6、7、8.
∴有三种购进方案:
| A型 | 6辆 | 7辆 | 8辆 |
| B型 | 10辆 | 9辆 | 8辆 |
点评 此题考查的知识点是一次函数的应用,关键是先根据已知列出不等式组得出方案,然后通过求最值及计算出费用得出答案.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:选择题
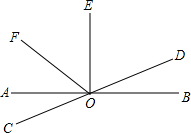 如图,直线AB、CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠BOD=15°,则下列结论中不正确的是( )
如图,直线AB、CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠BOD=15°,则下列结论中不正确的是( )| A. | ∠AOF=45° | B. | ∠AOD与∠BOD互为补角 | ||
| C. | ∠BOD=∠AOC | D. | ∠BOD的余角等于85° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A,B两点,且与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于C点,CD垂直于x轴,垂足为D,若OA=OB=OD=3,
如图所示,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A,B两点,且与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于C点,CD垂直于x轴,垂足为D,若OA=OB=OD=3,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\sqrt{3}$ | B. | $\sqrt{-3}$ | C. | $\sqrt{{{(-3)}^2}}$ | D. | $\root{3}{-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1≤y2 | B. | y1≥y2 | C. | y1<y2 | D. | y1>y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com