练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
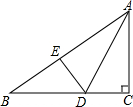
    2．如图，在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB，则下列结论错误的是（　　）
    A．△ADE≌△ADCB．DE=DCC．∠ADE=∠ADCD．BD=DC

    分析 先根据角平分线的性质得出DE=DC，进而证明△ADE≌△ADC，利用全等三角形的性质进行判断即可．

    解答 解：∵∠C=90°，AD平分∠BAC，DE⊥AB，
    ∴DE=DC，故B正确；
    ∵在Rt△ADE和Rt△ADC中，
    $\left\{\begin{array}{l}{AD=AD}\\{DE=DC}\end{array}\right.$
    ∴△ADE≌△ADC（HL），故A正确；
    ∴∠ADE=∠ADC，故C正确；
    但不能得出BD=DC，故D错误；
    故选D．

    点评 此题考查角平分线的性质，关键是利用角平分线的性质得出DE=DC，证明三角形全等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．在△ABC中，DE∥BC，若$\frac{AD}{BD}=\frac{1}{2}$，
    （1）DE=4，求BC；
    （2）△ABC的面积为18，求四边形DBEC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图是2012年11月份的日历，现用一长方形在日历中任意框出4个数，请用一个等式表示a，b，c，d之间的关系，下列表示正确的是（　　）
    A．a+d=b+cB．a+c=b+dC．a+b=c+dD．a+d+1=b+c

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．已知两个相似多边形的面积比是9：16，其中较小多边形的周长为36cm，则较大多边形的周长为（　　）
    A．48cmB．54cmC．56cmD．64cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．如图，在△ABC中，AC＞AB，DE（点D在△ABC的外部）垂直平分BC，交BC于点E，连接BD，CD，AD，过点D作DF⊥AC于点F，延长BA到点G，使得BG=CF，连接DG，若∠DBC-∠GBD=∠BCA，则下列说法中不正确的是（　　）
    A．∠BGD=90°B．AD平分∠GACC．∠GDB=∠FDCD．∠BDG=90°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．△ABC中，AB=BC，BE⊥AC于点E，AD⊥BC，∠BAD=45°，AD与BE交于点F，连接CF，
    （1）求证：BF=2AE；
    （2）若CD=$\sqrt{2}$，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知：如图，在正方形ABCD中，对角线AC与BD相交于点E，AF平分∠BAC，交BD于点F，求证：EF+AE=AB．

    查看答案和解析>>

    同步练习册答案