
【题目】平面直角坐标系中,![]() 是等边三角形,点
是等边三角形,点![]() ,点
,点![]() ,点
,点![]() 是
是![]() 边上的一个动点(与点
边上的一个动点(与点![]() 、
、![]() 不重合).直线
不重合).直线![]() 是经过点
是经过点![]() 的一条直线,把
的一条直线,把![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 的对应点是点
的对应点是点![]() .
.
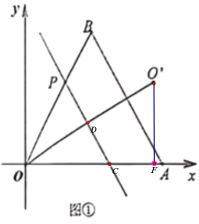
(1)如图①,当![]() 时,若直线
时,若直线![]() ,求点
,求点![]() 的坐标;
的坐标;
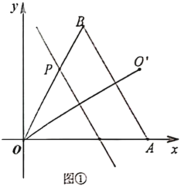
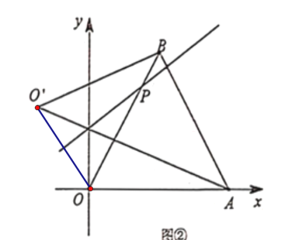
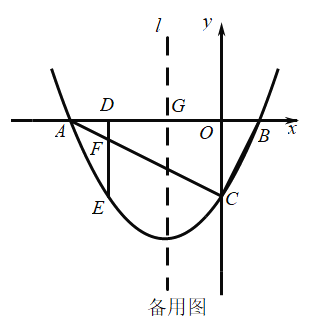
(2)如图②,当点![]() 在
在![]() 边上运动时,若直线
边上运动时,若直线![]() ,求
,求![]() 的面积;
的面积;
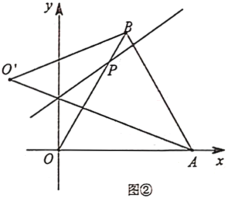
(3)当![]() 时,在直线
时,在直线![]() 变化过程中,求
变化过程中,求![]() 面积的最大值(直接写出结果即可).
面积的最大值(直接写出结果即可).
【答案】(1)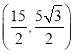 ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)设直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,再证明
,再证明![]() 是等边三角形;然后再根据
是等边三角形;然后再根据![]() ,
,![]() 、
、![]() 关于
关于![]() 对称,得到
对称,得到![]() ,
,![]() ;利用解直角三角形可以求得OD的长;过点
;利用解直角三角形可以求得OD的长;过点![]() 作
作![]() 于点
于点![]() ,在
,在![]() 中,解直角三角形可得OF和
中,解直角三角形可得OF和![]() 的长即可解答;
的长即可解答;
(2)连接![]() ,根据对称的性质和直线
,根据对称的性质和直线![]() 可得
可得![]() ,最后根据
,最后根据![]() 解答即可;
解答即可;
(3)作O’P⊥AB时,垂足为E,然后解三角形和线段的和差求得O’E,最后在运用三角形的面积公式求解即可.
解:(1)设直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∵![]() ,
,![]() ,
,![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,![]()
∵![]() ,
,
∴![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,在
,在![]() 中,可得
中,可得![]() ,
,
![]() ,
,
∴点![]() 的坐标为
的坐标为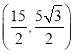
(2)连接![]() ,
,
∵![]() ,
,![]() 关于直线
关于直线![]() 对称,
对称,
∴![]() 直线
直线![]() ,
,
∵直线![]() ,
,
∴![]() ,
,
∴![]() .
.
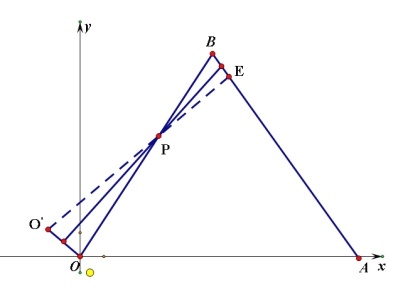
(3)当O’P⊥AB时,垂足为E,![]() 的面积最大
的面积最大
如图:作O’P⊥AB时,垂足为E
在Rt△BPE中,PA=2.∠B=60°
∴PE=PA·sin60°=![]()
∴O’E=6+![]() .
.
∴![]() 面积的最大值:
面积的最大值:![]() .
.


科目:初中数学 来源: 题型:
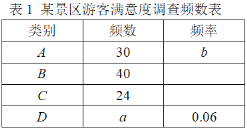
【题目】为了解游客对某景区的满意度,特对游客采取随机抽样的方式进行问卷调查,调查的结果分为A,B,C,D四类,其含意依次表示为“非常满意”、“比较满意”、“基本满意”和“不太满意”,划分类别后的数据整理如表1(不完整).
(1)求表中的数据a和b.
(2)如果根据表中频数画扇形统计图,那么类别为B的频数所对应的扇形圆心角是几度?
(3)已知该景区每日游客限流3000名,估计一天的游客中类别C的游客人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点M是平行四边形ABCD对角线AC所在直线上的一个动点(点M不与点A、C重合),分别过点A、C向直线BM作垂线,垂足分别为点E、F,点O为AC的中点.
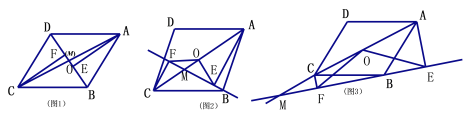
⑴如图1,当点M与点O重合时,OE与OF的数量关系是 .
⑵直线BM绕点B逆时针方向旋转,且∠OFE=30°.
①如图2,当点M在线段AC上时,猜想线段CF、AE、OE之间有怎样的数量关系?请你写出来并加以证明;
②如图3,当点M在线段AC的延长线上时,请直接写出线段CF、AE、OE之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 在平面直角坐标系中,
在平面直角坐标系中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 落在点
落在点![]() 处,得到
处,得到![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线交
轴的直线交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .
.![]() ,
,![]() .
.
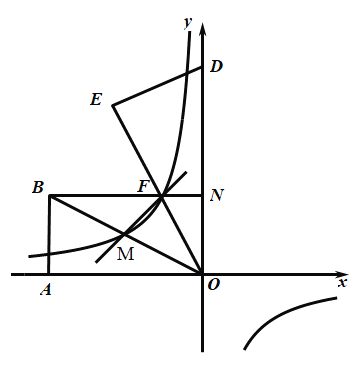
(1)求经过点![]() 、
、![]() 的反比例函数
的反比例函数![]() 和直线
和直线![]() :
:![]() 的解析式;
的解析式;
(2)过点![]() 作
作![]() 轴,求五边形
轴,求五边形![]() 的面积;
的面积;
(3)直接写出当![]() 时
时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
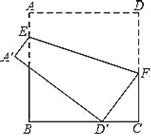
【题目】如图,正方形![]() 的边长是9,点
的边长是9,点![]() 是
是![]() 边上的一个动点,点
边上的一个动点,点![]() 是
是![]() 边上一点,
边上一点,![]() ,连接
,连接![]() ,把正方形
,把正方形![]() 沿
沿![]() 折叠,使点
折叠,使点![]() ,
,![]() 分别落在点
分别落在点![]() ,
,![]() 处,当点
处,当点![]() 落在线段
落在线段![]() 上时,线段
上时,线段![]() 的长为__________.
的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
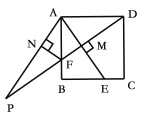
【题目】如图,正方形ABCD中,点E为BC边上的一点,连接AE,过点D作DM⊥AE,垂足为点M,交AB于点F.将△AMF沿AB翻折得到△ANF.延长DM,AN交于点P. 给出以下结论①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() ;.其中正确的是( )
;.其中正确的是( )
A.①②③④B.①②③C.①②④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求点![]() 的坐标和抛物线的函数关系式;
的坐标和抛物线的函数关系式;
(2)点![]() 是
是![]() 上一点(不与点
上一点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() ,交
,交![]() 于点
于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)设抛物线的对称轴![]() 交
交![]() 轴于点
轴于点![]() ,在(2)的条件下,点
,在(2)的条件下,点![]() 是抛物线对称轴上一点,点
是抛物线对称轴上一点,点![]() 是坐标平面内一点,是否存在点
是坐标平面内一点,是否存在点![]() 、
、![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请求出点
为顶点的四边形是菱形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
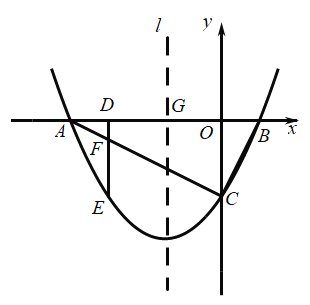
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小元步行从家去火车站,走到 6 分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3 分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )

A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com