
【题目】如图,在平面直角坐标系中,点A的坐标为(4,0),点B的坐标为(10,0),点C为平面上一动点,连接CA,CB,将线段CB绕点C逆时针旋转90°得到线段CD,当AC=4,线段AD的长取最大值时,点D的坐标为_____.
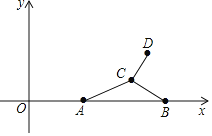
【答案】(4,6+4![]() ).
).
【解析】
作TA⊥AB,使得TA=AB.连接AD,BT,BD.首先证明点D的运动轨迹是以T为圆心4![]() 为半径的圆,推出当点D在AT的延长线上时,AD的值最大.
为半径的圆,推出当点D在AT的延长线上时,AD的值最大.
作TA⊥AB,使得TA=AB.连接AD,BT,BD.
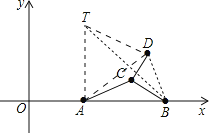
∵△ATB,△CDB都是等腰直角三角形,
∴BT=![]() AB,BD=
AB,BD=![]() BC,∠ABT=∠CBD=45°,
BC,∠ABT=∠CBD=45°,
∴![]() ,∠ABC=∠TBD,
,∠ABC=∠TBD,
∴△ABC∽△TBD,
∴![]() ,
,
∵A(4,0),B(10,0),AC=4,
∴AT=AB=6,DT=4![]() ,
,
∴T(4,6),
∴点D的运动轨迹是以T为圆心4![]() 为半径的圆,
为半径的圆,
∴当点D在AT的延长线上时,AD的值最大,最大值=6+4![]() ,
,
∴点D的坐标为(4,6+4![]() ) .
) .
故答案为:(4,6+4![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据:
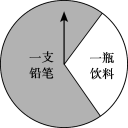
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 546 | 701 |
落在“铅笔”的频率 (结果保留小数点后两位) | 0.68 | 0.74 | 0.68 | 0.69 | 0.68 | 0.70 |
(1)转动该转盘一次,获得铅笔的概率约为_______;(结果保留小数点后一位)
(2)铅笔每只0.5元,饮料每瓶3元,经统计该商场每天约有4000名顾客参加抽奖活动,请计算该商场每天需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在3000元左右,则转盘上“一瓶饮料”区域的圆心角应调整为______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 于点D.
于点D.
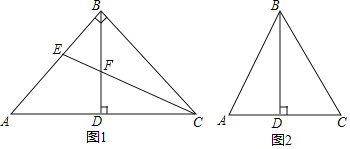
(1)如图1,当![]() 时,若CE平分
时,若CE平分![]() ,交AB于点E,交BD于点F.
,交AB于点E,交BD于点F.
①求证:![]() 是等腰三角形;
是等腰三角形;
②求证:![]() ;
;
(2)点E在AB边上,连接CE.若![]() ,在图2中补全图形,判断
,在图2中补全图形,判断![]() 与
与![]() 之间的数量关系,写出你的结论,并写出求解
之间的数量关系,写出你的结论,并写出求解![]() 与
与![]() 关系的思路.
关系的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,老师对大学说:“你任意想一个非零实数,然后按下列步骤操作,我会直接说出你运算的最后结果”
操作步骤如下:
第一步:计算这个数与1的和的平方,减去这个数与1的差的平方
第二步:把第一步得到的数乘以25
第三步:把第二步得到的数除以你想的这个数
(1)若小明同学心里想的是数9,请帮他计算出最后结果:
![]() .
.
(2)老师说:“同学们,无论你们心里想的是什么非零实数,按照以上步骤进行操作,得到的最后结果都相等”,小明同学想验证这个结论,于是,设心里想的数是a(a≠0),请你帮小明完成这个验证过程
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月23日是世界读书日,某校为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
数据收集:从全校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下(单位:![]() )
)
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据:按如下分段整理样本数据并补全表格:
课外阅读时间 |
|
|
|
|
等级 |
|
|
|
|
人数 | 3 |
| 8 |
|
分析数据:补全下列表格中的统计量:
平均数 | 中位数 | 众数 |
80 |
|
|
(1)![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)用样本中的统计量估计该校学生每周用于课外阅读时间的情况等级为 ;
(3)如果该校现有学生400人,估计等级为“![]() ”的学生有多少名?
”的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A![]() ,B(-1,2)是一次函数
,B(-1,2)是一次函数![]() 与反比例函数
与反比例函数![]()
(![]() )图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:如图(1),一圆柱的高为5dm,底面半径为5dm,BC是底面直径,求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线.小明设计了两条路线:
路线1:侧面展开图中的AC.如下图(2)所示:
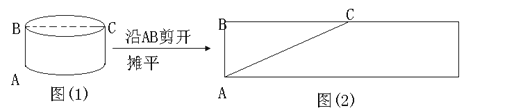
设路线1的长度为![]() ,则
,则![]() ,
,
路线2:高线AB + 底面直径BC.如上图(1)所示:
设路线2的长度为![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
所以要选择路线2较短.
(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1dm,高AB为5dm”继续按前面的路线进行计算.请你帮小明完成下面的计算:
路线1:![]() ___________________;
___________________;
路线2:![]() __________
__________
∵![]()
![]() ,
,
∴![]()
![]() (填>或<) 所以应选择路线_________(填1或2)较短.
(填>或<) 所以应选择路线_________(填1或2)较短.
(2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r,高为h时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到C点的路线最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 为二次函数
为二次函数![]() 的图象的顶点.
的图象的顶点.
(1)过点![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,求线段
,求线段![]() 的最小值;
的最小值;
(2)设正比例函数![]() 与上述二次函数的图象相交于点
与上述二次函数的图象相交于点![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b交x轴于点A(1,0) ,与双曲线![]() 交于点
交于点![]()
(1)求直线AB的解析式为____ ____________;
(2)若 x 轴上存在动点 M(m,0),过点 M 且与 x 轴垂直的直线与直线AB交于点C,与双曲线交于点D(C、D两点不重合),当BC >BD时,写出m的取值范围_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com