
 如图,△ABC的角平分线交于点O.
如图,△ABC的角平分线交于点O.分析 (1)先根据三角形的内角和定理求出∠BAC+∠BCA的度数,再根据角平分线的定义求出$\frac{1}{2}$(∠BAC+∠BCA),然后再利用三角形的内角和定理求解即可;
(2)方法同(1).
解答 解:(1)∵OA,OC分别是∠BAC,∠BCA的平分线,
∴∠OAC=$\frac{1}{2}$∠BAC,∠OCA=$\frac{1}{2}$∠BCA,
∴∠AOC=180°-∠OAC-∠OCA=180°-$\frac{1}{2}$∠BAC-$\frac{1}{2}$∠BCA,
=180°-$\frac{1}{2}$(∠BAC+∠BCA).
又∵∠B=60°,
∴∠BAC+∠BCA=180°-60°=120°.
∴$\frac{1}{2}$(∠BAC+∠BCA)=120°×$\frac{1}{2}$=60°.
∴∠AOC=180°-60°=120°,
当∠B=80°时,同理可得∠AOC=130°,
故答案为:120°,130°;
(1))∵OA,OC分别是∠BAC,∠BCA的平分线,
∴∠OAC=$\frac{1}{2}$∠BAC,∠OCA=$\frac{1}{2}$∠BCA,
∴∠AOC=180°-∠OAC-∠OCA=180°-$\frac{1}{2}$∠BAC-$\frac{1}{2}$∠BCA,
=180°-$\frac{1}{2}$(∠BAC+∠BCA).
∵∠B=α,
∴∠BAC+∠BCA=180°-α,
∴$\frac{1}{2}$(∠BAC+∠BCA)=$\frac{1}{2}$(180°-α)=90°-$\frac{1}{2}α$,
∴∠AOC=180°-(90°-$\frac{1}{2}$α)=90°+$\frac{1}{2}α$.
点评 本题考查的是三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | (3,2)与(2,3)表示的位置相同 | |
| B. | (a,b)与(b,a)表示的位置一定不同 | |
| C. | (3,-2),(-2,3)是表示不同位置的两个有序数对 | |
| D. | (4,4)与(4,4)表示两个不同的位置 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y=-2x2 | |||||||
| y=-2x2+1 | |||||||
| y=-2x2-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
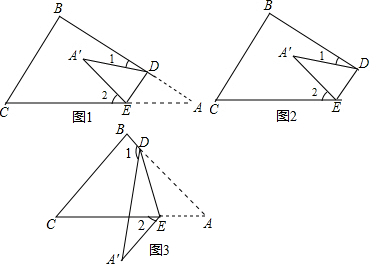
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com