
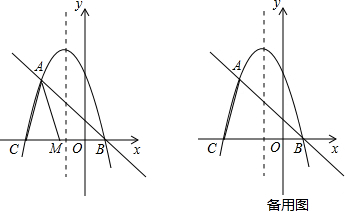
分析 (1)由梦想直线的定义可求得其解析式,联立梦想直线与抛物线解析式可求得A、B的坐标;
(2)当N点在y轴上时,过A作AD⊥y轴于点D,则可知AN=AC,结合A点坐标,则可求得ON的长,可求得N点坐标;当M点在y轴上即,M点在原点时,过N作NP⊥x轴于点P,由条件可求得∠NMP=60°,在Rt△NMP中,可求得MP和NP的长,则可求得N点坐标;
(3)当AC为平行四边形的一边时,过F作对称轴的垂线FH,过A作AK⊥x轴于点K,可证△EFH≌△ACK,可求得DF的长,则可求得F点的横坐标,从而可求得F点坐标,由HE的长可求得E点坐标;当AC为平行四边形的对角线时,设E(-1,t),由A、C的坐标可表示出AC中点,从而可表示出F点的坐标,代入直线AB的解析式可求得t的值,可求得E、F的坐标.
解答 解:
(1)∵抛物线y=-$\frac{2\sqrt{3}}{3}$x2-$\frac{4\sqrt{3}}{3}$x+2$\sqrt{3}$,
∴其梦想直线的解析式为y=-$\frac{2\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$,
联立梦想直线与抛物线解析式可得$\left\{\begin{array}{l}{y=-\frac{2\sqrt{3}}{3}x+\frac{2\sqrt{3}}{3}}\\{y=-\frac{2\sqrt{3}}{3}{x}^{2}-\frac{4\sqrt{3}}{3}x+2\sqrt{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-2}\\{y=2\sqrt{3}}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$,
∴A(-2,2$\sqrt{3}$),B(1,0),
故答案为:y=-$\frac{2\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$;(-2,2$\sqrt{3}$);(1,0);
(2)当点N在y轴上时,△AMN为梦想三角形,
如图1,过A作AD⊥y轴于点D,则AD=2,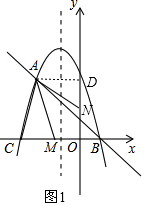
在y=-$\frac{2\sqrt{3}}{3}$x2-$\frac{4\sqrt{3}}{3}$x+2$\sqrt{3}$中,令y=0可求得x=-3或x=1,
∴C(-3,0),且A(-2,2$\sqrt{3}$),
∴AC=$\sqrt{(-2+3)^{2}+(2\sqrt{3})^{2}}$=$\sqrt{13}$,
由翻折的性质可知AN=AC=$\sqrt{13}$,
在Rt△AND中,由勾股定理可得DN=$\sqrt{A{N}^{2}-A{D}^{2}}$=$\sqrt{13-4}$=3,
∵OD=2$\sqrt{3}$,
∴ON=2$\sqrt{3}$-3或ON=2$\sqrt{3}$+3,
当ON=2$\sqrt{3}$+3时,则MN>OD>CM,与MN=CM矛盾,不合题意,
∴N点坐标为(0,2$\sqrt{3}$-3);
当M点在y轴上时,则M与O重合,过N作NP⊥x轴于点P,如图2,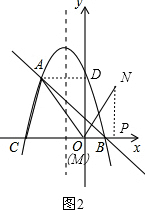
在Rt△AMD中,AD=2,OD=2$\sqrt{3}$,
∴tan∠DAM=$\frac{MD}{AD}$=$\sqrt{3}$,
∴∠DAM=60°,
∵AD∥x轴,
∴∠AMC=∠DAO=60°,
又由折叠可知∠NMA=∠AMC=60°,
∴∠NMP=60°,且MN=CM=3,
∴MP=$\frac{1}{2}$MN=$\frac{3}{2}$,NP=$\frac{\sqrt{3}}{2}$MN=$\frac{3\sqrt{3}}{2}$,
∴此时N点坐标为($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$);
综上可知N点坐标为(0,2$\sqrt{3}$-3)或($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$);
(3)①当AC为平行四边形的边时,如图2,过F作对称轴的垂线FH,过A作AK⊥x轴于点K,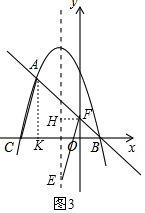
则有AC∥EF且AC=EF,
∴∠ACK=∠EFH,
在△ACK和△EFH中
$\left\{\begin{array}{l}{∠ACK=∠EFH}\\{∠AKC=∠EHF}\\{AC=EF}\end{array}\right.$
∴△ACK≌△EFH(AAS),
∴FH=CK=1,HE=AK=2$\sqrt{3}$,
∵抛物线对称轴为x=-1,
∴F点的横坐标为0或-2,
∵点F在直线AB上,
∴当F点横坐标为0时,则F(0,$\frac{2\sqrt{3}}{3}$),此时点E在直线AB下方,
∴E到y轴的距离为EH-OF=2$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$,即E点纵坐标为-$\frac{4\sqrt{3}}{3}$,
∴E(-1,-$\frac{4\sqrt{3}}{3}$);
当F点的横坐标为-2时,则F与A重合,不合题意,舍去;
②当AC为平行四边形的对角线时,
∵C(-3,0),且A(-2,2$\sqrt{3}$),
∴线段AC的中点坐标为(-2.5,$\sqrt{3}$),
设E(-1,t),F(x,y),
则x-1=2×(-2.5),y+t=2$\sqrt{3}$,
∴x=-4,y=2$\sqrt{3}$-t,
代入直线AB解析式可得2$\sqrt{3}$-t=-$\frac{2\sqrt{3}}{3}$×(-4)+$\frac{2\sqrt{3}}{3}$,解得t=-$\frac{4\sqrt{3}}{3}$,
∴E(-1,-$\frac{4\sqrt{3}}{3}$),F(-4,$\frac{10\sqrt{3}}{3}$);
综上可知存在满足条件的点F,此时E(-1,-$\frac{4\sqrt{3}}{3}$)、F(0,$\frac{2\sqrt{3}}{3}$)或E(-1,-$\frac{4\sqrt{3}}{3}$)、F(-4,$\frac{10\sqrt{3}}{3}$).
点评 本题为二次函数的综合应用,涉及函数图象的交点、勾股定理、轴对称的性质、平行四边形的性质、方程思想及分类讨论思想等知识.在(1)中理解题目中梦想直线的定义是解题的关键,在(2)中确定出N点的位置,求得ON的长是解题的关键,在(3)中确定出E、F的位置是解题的关键,注意分两种情况.本题考查知识点较多,综合性较强,难度较大.


科目:初中数学 来源: 题型:解答题
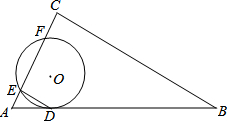 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为6,弧DE的长度为2π.
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为6,弧DE的长度为2π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
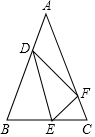 如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D、F分别在边AB、AC上.
如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D、F分别在边AB、AC上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
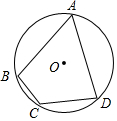 如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )
如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2米,∠BCA=30°,且B、C、D三点在同一直线上.
小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2米,∠BCA=30°,且B、C、D三点在同一直线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com