

| 3 |
|
|
|
| 3 |
| ||
| 3 |
|
|
|
| ||
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
| ||
| 3 |
|
|
|
| ||
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
| 3 |
|
|
|
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
| 3 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
<
 
练习册系列答案
相关习题
科目:初中数学 来源:不详 题型:解答题 如图,已知直线y=-
(1)请直接写出点C、D的坐标; (2)求抛物线L1的解析式; (3)若正方形以每秒
(4)在(3)的条件下,抛物线L1与正方形一起平移,同时停止,得到抛物线L2.两抛物线的顶点分别为M、N,点P是x轴上一动点,点Q是抛物线L1上一动点,是否存在这样的点P、Q,使得以M、N、P、Q为顶点的四边形为平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由. 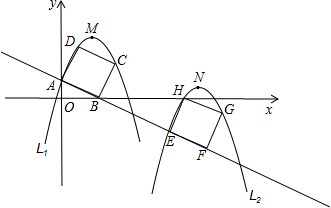 查看答案和解析>> 科目:初中数学 来源:不详 题型:解答题 已知:如图,抛物线y=ax2+bx+c(a≠O)经过X轴上的两点A(x1,0)、B(x2,0)和y轴上的点C(0,-
(1)求抛物线的解析式; (2)设D在抛物线上,且C,D两点关于抛物线的对称轴对称,问直线BD是否经过圆心P,  并说明理由; 并说明理由;(3)设直线BD交⊙P于另一点E,求经过E点的⊙P的切线的解析式. 查看答案和解析>> 科目:初中数学 来源:不详 题型:解答题 天羽服装厂生产M、N型两种服装,受资金及规模限制,每天最多只能用A种面料68米  和B种面料62米生产M、N型两种服装共80套.已知M、N型服装每套所需面料和成本如下表,设每天生产M型服装x套. 和B种面料62米生产M、N型两种服装共80套.已知M、N型服装每套所需面料和成本如下表,设每天生产M型服装x套.
(2)经市场调查,生产的M、N型服装有两种销售方案(假设每天生产的服装都能全部售出). 方案Ⅰ:两种型号服装都在本市销售,M型180元/件、N型120元/件; 方案Ⅱ:N型服装在本市销售,120元/件,M型服装批发给H市服装商,其每件的批发价y(元)与批量x(件)之间的关系如图所示. 如果你是厂长,应采用哪种销售方案可使每天获利最大,最大利润是多少?并确定相应的生产方案. 查看答案和解析>> 科目:初中数学 来源:不详 题型:解答题 已知抛物线y=ax2+bx-1经过点A(一1,0)、B(m,0)(m>0),且与y轴交于点C (1)求抛物线对应的函数表达式(用含m的式子表示); (2)如图,⊙M经过A、B、C三点,求扇形MBC(阴影部分)的面积S(用含m的式子表示); (3)若抛物线上存在点P,使得△APB∽△ABC,求m的值. 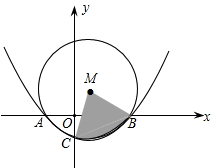 查看答案和解析>> 科目:初中数学 来源:不详 题型:填空题 已知二次函数y=ax2+bx+c(a≠0)的顶点坐标(-1,-3.2)及部分图象(如图),由图象可知关于x的方程ax2+bx+c=0的两个根分别是x1=1.3和x2=______. 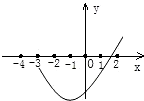 查看答案和解析>> 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |