
����Ŀ���Ķ�һ�����֣��ٻش��������⣺��֪��ƽ�������������Ϊ![]() ��
��![]() ������������빫ʽΪ
������������빫ʽΪ![]() ��ͬʱ����������ͬһ�������ϻ�����ֱ��ƽ����
��ͬʱ����������ͬһ�������ϻ�����ֱ��ƽ����![]() �ᡢƽ����
�ᡢƽ����![]() ��ʱ�������ľ��빫ʽ�ɻ����
��ʱ�������ľ��빫ʽ�ɻ����![]() ��
��![]() ��
��
��1������֪����![]() ��
��![]() ������
������![]() �����ľ��룻
�����ľ��룻
��2����֪��![]() ��ƽ����
��ƽ����![]() ���ֱ���ϣ���
���ֱ���ϣ���![]() ��������Ϊ7����
��������Ϊ7����![]() ��������Ϊ
��������Ϊ![]() ������
������![]() �����ľ��룻
�����ľ��룻
��3����֪һ�������θ����������Ϊ![]() ��
��![]() ��
��![]() �������ж��������Ƿ��ߣ���������˵�����ɣ��������������ͼ�ε������
�������ж��������Ƿ��ߣ���������˵�����ɣ��������������ͼ�ε������
���𰸡���1��![]() ����2��9����3��A��B��C���㲻���ߣ���ABC�����Ϊ
����2��9����3��A��B��C���㲻���ߣ���ABC�����Ϊ![]() ��
��
��������
��1�����������ľ��빫ʽ���м��㼴�ɣ�
��2�����ݵ�M��N��ƽ����y���ֱ���ϣ��������������ľ��빫ʽ![]() ���м��㣻
���м��㣻
��3�������A��B��C�����У���������֮��ľ��룬���жϳ����㲻���ߣ���һ�����ж�������ABC����״���Ӷ�������������
�⣺��1���ߵ�A��3��3����B��-2��-1����
��AB=![]() ��
��
��A��B�����ľ�����![]() ��
��
��2���ߵ�M��N��ƽ����y���ֱ���ϣ���M��������Ϊ7����N��������Ϊ-2��
��MN=|-2-7|=9��
��M��N�����ľ�����9��
��3�������㲻���ߣ���������Ϊֱ�������Σ��������£�
��һ�������θ����������Ϊ![]() ��
��
��AB=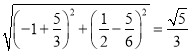 ��
��
AC=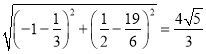 ��
��
BC=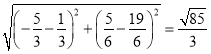 ��
��
��A��B��C���㲻���ߣ�
��AB2+AC2=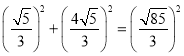 =BC2��
=BC2��
���ABC��ֱ�������Σ�
��S��ABC=![]() ABAC=
ABAC=![]() ��
��
��A��B��C���㲻���ߣ���ABC�����Ϊ![]() ��
��


 Сѧ�������Ծ�ϵ�д�
Сѧ�������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
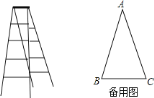
����Ŀ����ͼ����һ������װ���������ݣ���£ʱ�����ӵij�Ϊ![]() �ף�����飬�����������Ž�Ϊ
�ף�����飬�����������Ž�Ϊ![]() ʱ�ȫ��
ʱ�ȫ��
��1���������ȫʱ�������ܴﵽ�����߶��Ƕ��٣�����ȷ��![]() �ף�
�ף�
��2��װ��ʱ�������������![]() �ף�һ���������������ʱ�������ֱ��ܴﵽ�����߶ȱ�������˸߳�
�ף�һ���������������ʱ�������ֱ��ܴﵽ�����߶ȱ�������˸߳�![]() �ף�Ҫʹװ���������У���ô�����Ž�����Ϊ���ٶȣ�����ȷ��
�ף�Ҫʹװ���������У���ô�����Ž�����Ϊ���ٶȣ�����ȷ��![]() �ȣ�
�ȣ�
���ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ת�̱����ֳ�������ͬ��С�����Σ����ֱ����1��2��3��4��5��6���������֣�ָ��ͣ��ÿ�����εĿ�������ȡ���λͬѧ���Է������������⣺
�ף����ָ��ǰ���ζ�ͣ����3�����Σ��´ξ�һ������ͣ��3�����Σ�
�ң�ֻҪָ������ת���Σ�һ������һ��ͣ��6�����Σ�
����ָ��ͣ�����������εĸ�����ͣ��ż�������εĸ�����ȣ�
���������õ�ʱ��ֻҪ��ת��ǰĬĬ�����ָ��ͣ��6�����Σ�ָ��ͣ��6�����εĿ����Ծͻ�Ӵ�

���У�����Ϊ��ȷ�ļ����У� ��
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
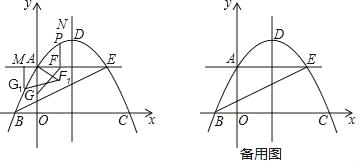
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y����![]() x2+bx+c��x�ύ�ڵ�A��B����y�ύ�ڵ�C��ֱ��BC�Ľ���ʽΪy����x+6��
x2+bx+c��x�ύ�ڵ�A��B����y�ύ�ڵ�C��ֱ��BC�Ľ���ʽΪy����x+6��
(1)�������ߵĽ���ʽ��
(2)��MΪ�߶�BC�Ϸ��������ϵ�����һ�㣬����MB��MC����NΪ�����߶Գ���������һ�㣬��M��ֱ��BC�ľ������ʱ�����M�����꼰MN+NB����Сֵ��
(3)��(2)�У���M��ֱ��BC�ľ������ʱ������OM��BC�ڵ�E����ԭ������������OMƽ�ƣ�ƽ�ƺ��������Ϊy�䣬��y�侭����Mʱ�����ĶԳ�����x��Ľ����ΪH������BOE�Ƶ�B��ʱ����ת60������BO1E1���ٽ���BO1E1����ֱ��O1Hƽ�ƣ��õ���B1O2E2����ƽ�����Ƿ���ڵ�F��ʹ�Ե�C��H��B1��FΪ������ı�������B1HΪ�ߵ����Σ������ڣ�ֱ��д����B1�ĺ����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ΪD��������y����![]() x2+
x2+![]() x+4��y�ύ�ڵ�A����x�ύ������B��C����B�ڵ�C����ߣ�����A���E���������ߵĶԳ���Գƣ���B��E��ֱ��y��kx+b��k��bΪ�������ϣ�
x+4��y�ύ�ڵ�A����x�ύ������B��C����B�ڵ�C����ߣ�����A���E���������ߵĶԳ���Գƣ���B��E��ֱ��y��kx+b��k��bΪ�������ϣ�
(1)��k��b��ֵ��
(2)��PΪֱ��AE�Ϸ��������ϵ�����һ�㣬����P��AE�Ĵ��߽�AE�ڵ�F����GΪy��������һ�㣬����PBE��������ʱ����PF+FG+![]() OG����Сֵ��
OG����Сֵ��
(3)��(2)�У���PF+FG+![]() OGȡ����Сֵʱ������AFG�Ƶ�A��˳ʱ������ת30���õ���AF1G1������G1��AE�Ĵ�����AE���ڵ�M����D����ƽ��
OGȡ����Сֵʱ������AFG�Ƶ�A��˳ʱ������ת30���õ���AF1G1������G1��AE�Ĵ�����AE���ڵ�M����D����ƽ��![]() ����λ���Ⱥ������N�غϣ���QΪֱ��DN������һ�㣬��ƽ��ֱ������ϵ���Ƿ����һ��S��ʹ��S��Q��M��NΪ������MNΪ�ߵ��ı���Ϊ���Σ������ڣ�ֱ��д����S�����ꣻ�������ڣ���˵�����ɣ�
����λ���Ⱥ������N�غϣ���QΪֱ��DN������һ�㣬��ƽ��ֱ������ϵ���Ƿ����һ��S��ʹ��S��Q��M��NΪ������MNΪ�ߵ��ı���Ϊ���Σ������ڣ�ֱ��д����S�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��![]() �У�
�У�![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��
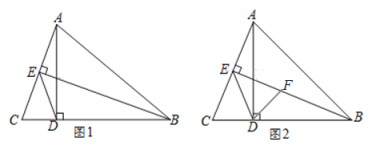
��1����![]() ��
��![]() ��
��![]() ����
����![]() ���ܳ���
���ܳ���
��2����ͼ2����![]() ��
��![]() ��
��![]() �Ľ�ƽ����
�Ľ�ƽ����![]() ��
��![]() �ڵ�
�ڵ�![]() ����֤��
����֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
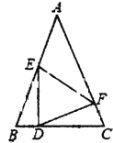
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ���ϵ�һ�㣬
���ϵ�һ�㣬![]() ����
����![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��1��![]() �ǵ�������������˵�����ɣ�
�ǵ�������������˵�����ɣ�
��2������![]() ����
����![]() ��ʱ��
��ʱ��![]() �ǵȱ������Σ�
�ǵȱ������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
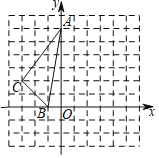
����Ŀ����ͼ�������У�ÿ��С�����εı߳����ǵ�λ1����ABC��ƽ��ֱ������ϵ�е�λ����ͼ��
��1����������ABC����ƽ��2����λ�õ���A1B1C1��
��2����������ABC�Ƶ�O˳ʱ�뷽����ת90���õ��ġ�A2B2C2��
��3����x������һ��P�������P����C1��C2����֮����С�������P������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
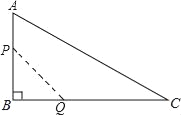
����Ŀ����ͼ���ڡ�ABC�У���B��90�㣬AB��12mm��BC��24mm������P�ӵ�A��ʼ�ر�AB��B��2mm/s���ٶ��ƶ��������B�غϣ�������Q�ӵ�B��ʼ�ر�BC��C��4mm/s���ٶ��ƶ��������C�غϣ������P��Q�ֱ��A��Bͬʱ���������˶���ʱ��Ϊxs���ı���APQC�����Ϊymm2��
��1��y��x֮��ĺ�����ϵʽ��
��2�����Ա���x��ȡֵ��Χ��
��3���ı���APQC������ܷ����172mm2�����ܣ�����˶���ʱ�䣻�����ܣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com