
”¾ĢāÄæ”æČēĶ¼£¬µćC½«Ļ߶ĪAB·Ö³ÉĮ½²æ·Ö£¬ČōAC2£½BCAB(AC£¾BC)£¬Ōņ³ĘµćCĪŖĻ߶ĪABµÄ»Ę½š·Öøīµć.ijŹżŃ§ŠĖȤŠ”×éŌŚ½ųŠŠÅ×ĪļĻßæĪĢāŃŠ¾æŹ±£¬ÓÉ»Ę½š·ÖøīµćĮŖĻėµ½”°»Ę½šÅ×ĪļĻß”±£¬ĄąĖʵŲøų³ö”°»Ę½šÅ×ĪļĻß”±µÄ¶ØŅå£ŗČōÅ×ĪļĻßy£½ax2+bx+c£¬Āś×ćb2£½ac(b”Ł0)£¬Ōņ³Ę“ĖÅ×ĪļĻßĪŖ»Ę½šÅ×ĪļĻß.
(¢ń)Čōij»Ę½šÅ×ĪļĻߵĶŌ³ĘÖįŹĒÖ±Ļßx£½2£¬ĒŅÓėyÖį½»ÓŚµć(0£¬8)£¬ĒóyµÄ×īŠ”Öµ£»
(¢ņ)Čō»Ę½šÅ×ĪļĻßy£½ax2+bx+c(a£¾0)µÄ¶„µćPĪŖ(1£¬3)£¬°ŃĖüĻņĻĀĘ½ŅĘŗóÓėxÖį½»ÓŚA(![]() +3£¬0)£¬B(x0£¬0)£¬ÅŠ¶ĻŌµćŹĒ·ńŹĒĻ߶ĪABµÄ»Ę½š·Öøīµć£¬²¢ĖµĆ÷ĄķÓÉ.
+3£¬0)£¬B(x0£¬0)£¬ÅŠ¶ĻŌµćŹĒ·ńŹĒĻ߶ĪABµÄ»Ę½š·Öøīµć£¬²¢ĖµĆ÷ĄķÓÉ.
![]()
”¾“š°ø”æ(¢ń)yÓŠ×īŠ”ÖµĪŖ6£»(¢ņ)ŌµćŹĒĻ߶ĪABµÄ»Ę½š·Öøīµć£¬ĄķÓɼū½āĪö.
”¾½āĪö”æ
(¢ń)øł¾Ż¶Ō³ĘÖįČ·¶ØaŗĶbµÄ¹ŲĻµ£¬ŌŁøł¾ŻŅŃÖŖĢõ¼ž¼“æÉĒó½ā£»
(¢ņ)øł¾ŻÅ×ĪļĻߵĶ„µć×ų±źČ·¶Øx0µÄÖµ£¬ŌŁøł¾Ż»Ę½š·ÖøīµÄ¶ØŅ弓æÉÅŠ¶Ļ.
(¢ń)”ß»Ę½šÅ×ĪļĻߵĶŌ³ĘÖįŹĒÖ±Ļßx£½2£¬
”ą©![]() £½2£¬
£½2£¬
”ąb£½©4a£¬ÓÖb2£½ac
”ą16a2£½ac.
ĒŅÓėyÖį½»ÓŚµć(0£¬8)£¬
”ąc£½8.
”ąa£½![]() £¬b£½©2.
£¬b£½©2.
”ąy£½![]() x2©2x+8
x2©2x+8
£½![]() (x©2)2+6£¬
(x©2)2+6£¬
”ß![]() £¾0£¬
£¾0£¬
”ąyÓŠ×īŠ”ÖµĪŖ6.
(¢ņ)ŌµćŹĒĻ߶ĪABµÄ»Ę½š·Öøīµć.ĄķÓÉČēĻĀ£ŗ
”ß»Ę½šÅ×ĪļĻßy£½ax2+bx+c(a£¾0)µÄ¶„µćPĪŖ(1£¬3)£¬
°ŃĖüĻņĻĀĘ½ŅĘŗóÓėxÖį½»ÓŚA(![]() +3£¬0)£¬B(x0£¬0)£¬
+3£¬0)£¬B(x0£¬0)£¬
”ąx0£½©1©![]() .
.
”ąOA£½3+![]() £¬OB£½1+
£¬OB£½1+![]() £¬AB£½4+2
£¬AB£½4+2![]() .
.
OA2£½(3+![]() )2£½14+6
)2£½14+6![]() .
.
OBAB£½(1+![]() )(4+2
)(4+2![]() )£½14+6
)£½14+6![]() .
.
”ąOA2£½OBAB.
”ąŌµćŹĒĻ߶ĪABµÄ»Ę½š·Öøīµć.



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCµÄµćA£¬CŌŚ”ŃOÉĻ£¬”ŃOÓėABĻą½»ÓŚµćD£¬Į¬½ÓCD£¬”ĻA£½30”ć£¬DC£½![]() £®
£®
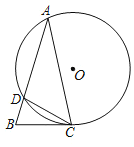
£Ø1£©ĒóŌ²ŠÄOµ½ĻŅDCµÄ¾ąĄė£»
£Ø2£©Čō”ĻACB+”ĻADC£½180”ć£¬ĒóÖ¤£ŗBCŹĒ”ŃOµÄĒŠĻߣ®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
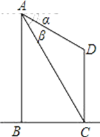
”¾ĢāÄæ”æČēĶ¼£¬Į½½ØÖžĪļµÄĖ®Ę½¾ąĄė![]() ĪŖ
ĪŖ![]() ,“Ó
,“Ó![]() µć²āµĆ
µć²āµĆ![]() µćµÄø©½Ē
µćµÄø©½Ē![]() ĪŖ
ĪŖ![]() £¬²āµĆ
£¬²āµĆ![]() µćµÄø©½Ē
µćµÄø©½Ē![]() ĪŖ
ĪŖ![]() ,ĒóÕāĮ½øö½ØÖžĪļµÄøß¶Č£®(
,ĒóÕāĮ½øö½ØÖžĪļµÄøß¶Č£®(![]() ½į¹ū±£ĮōÕūŹż)
½į¹ū±£ĮōÕūŹż)
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
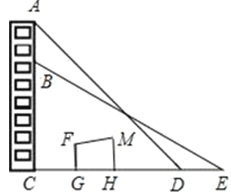
”¾ĢāÄæ”æŅ»“±Ā„µÄĀ„¶„¶Ė¹Ņ×ÅŅ»·ł³¤10Ć׵Ċū“«Ģõ·łAB£¬Ä³ŹżŃ§ŠĖȤŠ”×éŌŚŅ»“Ī»ī¶ÆÖŠ£¬×¼±ø²āĮæøĆĀ„µÄøß¶Č£¬µ«±»½ØÖžĪļFGHMµ²×”£¬²»ÄÜÖ±½Óµ½“ļĀ„µÄµ×²æ£¬ĖūĆĒŌŚµćD“¦²āµĆĢõ·ł¶„¶ĖAµÄŃö½Ē”ĻCDA£½45”ć£¬ĻņŗóĶĖ8Ć×µ½Eµć£¬²āµĆĢõ·łµ×¶ĖBµÄŃö½Ē”ĻCEB£½30”ć£ØµćC£¬D£¬EŌŚĶ¬Ņ»Ö±ĻßÉĻ£¬EC”ĶAC£©£®ĒėÄćøł¾ŻŅŌÉĻŹż¾Ż£¬°ļÖśøĆŠĖȤŠ”×é¼ĘĖćĀ„øßAC£Ø½į¹ū¾«Č·µ½0.01Ć×£¬²Īæ¼Źż¾Ż£ŗ![]() ”Ö1.732£¬
”Ö1.732£¬![]() ”Ö1.414£©£®
”Ö1.414£©£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
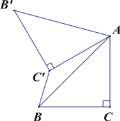
”¾ĢāÄæ”æČēĶ¼ £¬ŅŃÖŖ”÷ABC ÖŠ£¬”ĻC£½90”ć£¬AC£½BC£½![]() £¬½«”÷ABC Čʵć A Ė³Ź±Õė·½ĻņŠż×Ŗ 60”ćµĆµ½”÷A”äB”äC”äµÄĪ»ÖĆ£¬Į¬½Ó C”äB£¬Ōņ C”äB µÄ³¤ĪŖ ( )
£¬½«”÷ABC Čʵć A Ė³Ź±Õė·½ĻņŠż×Ŗ 60”ćµĆµ½”÷A”äB”äC”äµÄĪ»ÖĆ£¬Į¬½Ó C”äB£¬Ōņ C”äB µÄ³¤ĪŖ ( )
A.2£![]() B.
B.![]() C.
C.![]() D.1
D.1
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Š”Ć÷ĄūÓĆĖłŃ§ŹżŃ§ÖŖŹ¶²āĮæij½ØÖžĪļBCøß¶Č£¬²ÉÓĆĮĖČēĻĀµÄ·½·Ø£ŗŠ”Ć÷“ÓÓėij½ØÖžĪļµ×¶ĖBŌŚĶ¬Ņ»Ė®Ę½ĻßÉĻµÄAµć³ö·¢£¬ĻČŃŲŠ±ĘĀADŠŠ×ß260Ć×ÖĮĘĀ¶„D“¦£¬ŌŁ“ÓD“¦ŃŲĖ®Ę½·½Ļņ¼ĢŠųĒ°ŠŠČōøÉĆ×ŗóÖĮµćE“¦£¬ŌŚEµć²āµĆøĆ½ØÖžĪļ¶„¶ĖCµÄŃö½ĒĪŖ72”ć£¬½ØÖžĪļµ×¶ĖBµÄø©½ĒĪŖ63”ć£¬ĘäÖŠµćA”¢B”¢C”¢D”¢EŌŚĶ¬Ņ»Ę½ĆęÄŚ£¬Š±ĘĀADµÄĘĀ¶Či=1£ŗ2.4£¬øł¾ŻŠ”Ć÷µÄ²āĮæŹż¾Ż£¬¼ĘĖćµĆ³ö½ØÖžĪļBCµÄø߶ČŌ¼ĪŖ£Ø £©ĆףؼĘĖć½į¹ū¾«DEČ·µ½0.1Ć×£¬²Īæ¼Źż¾Ż£ŗsin72”ć”Ö0.95£¬tan72”ć”Ö3.08£¬sin63”ć”Ö0.89£¬tan63”ć”Ö1.96£©
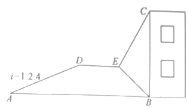
A.157.1 B.157.4 C.257.4 D.257.1
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÉč![]() ŹĒČĪŅāĮ½øö²»µČŹµŹż£¬ĪŅĆĒ¹ę¶Ø£ŗĀś×ć²»µČŹ½
ŹĒČĪŅāĮ½øö²»µČŹµŹż£¬ĪŅĆĒ¹ę¶Ø£ŗĀś×ć²»µČŹ½![]() µÄŹµŹż
µÄŹµŹż![]() µÄĖłÓŠČ”ÖµµÄČ«Ģ彊×ö±ÕĒų¼ä£¬±ķŹ¾ĪŖ
µÄĖłÓŠČ”ÖµµÄČ«Ģ彊×ö±ÕĒų¼ä£¬±ķŹ¾ĪŖ![]() £®¶ŌÓŚŅ»øöŗÆŹż£¬Čē¹ūĖüµÄ×Ō±äĮæ
£®¶ŌÓŚŅ»øöŗÆŹż£¬Čē¹ūĖüµÄ×Ō±äĮæ![]() ÓėŗÆŹżÖµ
ÓėŗÆŹżÖµ![]() Āś×ć£ŗµ±
Āś×ć£ŗµ±![]() Ź±£¬ÓŠ
Ź±£¬ÓŠ![]() £¬ĪŅĆĒ¾Ķ³Ę“ĖŗÆŹżŹĒ±ÕĒų¼ä
£¬ĪŅĆĒ¾Ķ³Ę“ĖŗÆŹżŹĒ±ÕĒų¼ä![]() ÉĻµÄ”°±ÕŗÆŹż”±£®ČēŗÆŹż
ÉĻµÄ”°±ÕŗÆŹż”±£®ČēŗÆŹż![]() £¬µ±
£¬µ±![]() Ź±£¬
Ź±£¬![]() £»µ±
£»µ±![]() Ź±£¬
Ź±£¬![]() £¬¼“µ±
£¬¼“µ±![]() Ź±£¬ÓŠ
Ź±£¬ÓŠ![]() £¬ĖłŅŌĖµŗÆŹż
£¬ĖłŅŌĖµŗÆŹż![]() ŹĒ±ÕĒų¼ä
ŹĒ±ÕĒų¼ä![]() ÉĻµÄ”°±ÕŗÆŹż”±
ÉĻµÄ”°±ÕŗÆŹż”±
£Ø1£©·“±ČĄżŗÆŹż![]() ŹĒ±ÕĒų¼ä
ŹĒ±ÕĒų¼ä![]() ÉĻµÄ”°±ÕŗÆŹż”±Āš?ĒėÅŠ¶Ļ²¢ĖµĆ÷ĄķÓÉ£»
ÉĻµÄ”°±ÕŗÆŹż”±Āš?ĒėÅŠ¶Ļ²¢ĖµĆ÷ĄķÓÉ£»
£Ø2£©Čō¶ž“ĪŗÆŹż![]() ŹĒ±ÕĒų¼ä
ŹĒ±ÕĒų¼ä![]() ÉĻµÄ”°±ÕŗÆŹż”±£¬Ēó
ÉĻµÄ”°±ÕŗÆŹż”±£¬Ēó![]() µÄÖµ£»
掙术
£Ø3£©ČōŅ»“ĪŗÆŹż![]() ŹĒ±ÕĒų¼ä
ŹĒ±ÕĒų¼ä![]() ÉĻµÄ”°±ÕŗÆŹż”±£¬Ēó“ĖŗÆŹżµÄ±ķ“ļŹ½(æÉÓĆŗ¬
ÉĻµÄ”°±ÕŗÆŹż”±£¬Ēó“ĖŗÆŹżµÄ±ķ“ļŹ½(æÉÓĆŗ¬![]() µÄ“śŹżŹ½±ķŹ¾)£®
µÄ“śŹżŹ½±ķŹ¾)£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
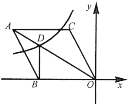
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ĮāŠĪ![]() µÄ¶„µć
µÄ¶„µć![]() ŌŚ×ų±źŌµć£¬±ß
ŌŚ×ų±źŌµć£¬±ß![]() ŌŚ
ŌŚ![]() ÖįµÄøŗ°ėÖįÉĻ£¬
ÖįµÄøŗ°ėÖįÉĻ£¬![]() £¬¶„µć
£¬¶„µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() £¬·“±ČĄżŗÆŹż
£¬·“±ČĄżŗÆŹż![]() µÄĶ¼ĻóÓėĮāŠĪ¶Ō½ĒĻß
µÄĶ¼ĻóÓėĮāŠĪ¶Ō½ĒĻß![]() ½»ÓŚµć
½»ÓŚµć![]() £¬Į¬½Ó”¢
£¬Į¬½Ó”¢![]() £¬µ±
£¬µ±![]() ÖįŹ±£¬
ÖįŹ±£¬![]() µć×ų±źĪŖ________£¬
µć×ų±źĪŖ________£¬![]() µÄÖµŹĒ_____£®
µÄÖµŹĒ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
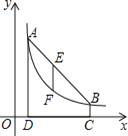
”¾ĢāÄæ”æČēĶ¼£¬µć![]() £¬
£¬![]() ŌŚ·“±ČĄżŗÆŹż
ŌŚ·“±ČĄżŗÆŹż![]() µÄĶ¼ĻóÉĻ£¬
µÄĶ¼ĻóÉĻ£¬![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬
£¬![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬
£¬![]() £®
£®
£Ø1£©Ēó![]() £¬
£¬![]() µÄÖµŗĶ·“±ČĄżŗÆŹżµÄ½āĪöŹ½£»
µÄÖµŗĶ·“±ČĄżŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©Į¬½Ó![]() £¬
£¬![]() ŹĒĻ߶Ī
ŹĒĻ߶Ī![]() ÉĻŅ»µć£¬¹żµć
ÉĻŅ»µć£¬¹żµć![]() ×÷
×÷![]() ÖįµÄ“¹Ļߣ¬½»·“±ČĄżŗÆŹżĶ¼ĻóÓŚµć
ÖįµÄ“¹Ļߣ¬½»·“±ČĄżŗÆŹżĶ¼ĻóÓŚµć![]() £¬Čō
£¬Čō![]() £¬Ēóµć
£¬Ēóµć![]() µÄ×ų±ź£®
µÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com