Question

12．如图，矩形OABC在平面直角坐标系内（O为坐标原点），点A在x轴上，点C在y轴上，点B的坐标为（-4，-4$\sqrt{3}$），点E是BC的中点，现将矩形折叠，折痕为EF，点F为折痕与y轴的交点，EF交x轴于G且使∠CEF=60°．
（1）求证：△EFC≌△GFO；
（2）求点D的坐标；
（3）若点P（x，y）是线段EG上的一点，设△PAF的面积为s，求s与x的函数关系式并写出x的取值范围．

Answer 1

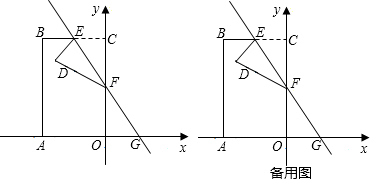
分析 （1）先从B的坐标表示BC和OC的长，从点E为中点表示EC的长，根据60度的正切值得CF的长，依次可得OG、OF的长，根据两边及其夹角对应相等的两三角形全等得结论；
（2）如图2，构建矩形MNOC，分别计算DM、DN和MC的长，即可以表示D的坐标；
（3）分两种情况讨论：
①当-2≤x＜0时P在线段EF上，如图3，
①当0＜x≤2时，P在线段FG上，如图4，
利用面积差可以表示s与x的关系式．

解答 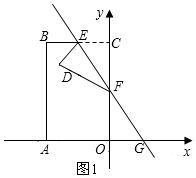证明：（1）如图1，在矩形OABC中，
∵点B的坐标为（-4，-4$\sqrt{3}$），
∴∠BCO=90°，BC=4，OC=4$\sqrt{3}$，
∵E是BC的中点，
∴EC=$\frac{1}{2}$BC=2，
Rt△ECF中，∵∠CEF=60°，
∴tan60°=$\frac{CF}{CE}=\sqrt{3}$，∠EFC=30°，
∴CF=2$\sqrt{3}$，
∴OF=4$\sqrt{3}$-2$\sqrt{3}$=2$\sqrt{3}$，
∴∠OFG=∠EFC=30°，
tan30°=$\frac{OG}{OF}$=$\frac{\sqrt{3}}{3}$，
∴OG=2$\sqrt{3}×\frac{\sqrt{3}}{3}$=2，
∴EC=OG=2，∠ECF=∠FOG=90°，CF=OF=2$\sqrt{3}$，
∴△EFC≌△GFO；

（2）如图2，过D作DM⊥BC，延长MD交x轴于N，
∵四边形MNOC是矩形，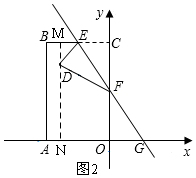
∴MN=CO=4$\sqrt{3}$，
∵折痕为EF，
∴△EFC≌△EFD，
∴DE=CE=2，∠DEF=∠CEF=60°，
∴∠MED=60°，
∴∠MDE=30°，
∴ME=1，
∴DM=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$，
∴MC=2=1=3，DN=4$\sqrt{3}$-$\sqrt{3}$=3$\sqrt{3}$，
∴D（-3，3$\sqrt{3}$）；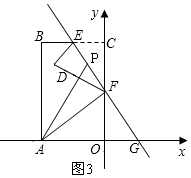

（3）∵EC=2，CF=OF=2$\sqrt{3}$
∴F（0，2$\sqrt{3}$），E（-2，4$\sqrt{3}$），
设直线EF的解析式为：y=kx+b，
则$\left\{\begin{array}{l}{b=2\sqrt{3}}\\{-2k+b=4\sqrt{3}}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-\sqrt{3}}\\{b=2\sqrt{3}}\end{array}\right.$，
∴直线EF的解析式为：y=-$\sqrt{3}$x+2$\sqrt{3}$，
由（1）得：△EFC≌△GFO，
∴OG=EC=2，AG=4+2=6，
当-2≤x＜0时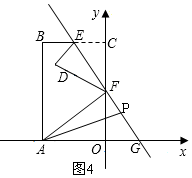，P在线段EF上，如图3，
∵s=S_△PAF=S_△PAG-S_△FAG=$\frac{1}{2}×6y$-$\frac{1}{2}$×$6×2\sqrt{3}$，
=3y-6$\sqrt{3}$，
=3（$\sqrt{3}$x+2$\sqrt{3}$）-6$\sqrt{3}$，
=-3$\sqrt{3}$x，
当0＜x≤2时，P在线段FG上，如图4，
s=S_△PAF=S_△AFG-S_△APG，
=$\frac{1}{2}$×6×2$\sqrt{3}$-$\frac{1}{2}$×6y，
=6$\sqrt{3}$-3（-$\sqrt{3}$x+2$\sqrt{3}$），
=3$\sqrt{3}$x；
综上所述，s与x的函数关系式为：$\left\{\begin{array}{l}{s=-3\sqrt{3}x（-2≤x＜0）}\\{s=3\sqrt{3}x（0＜x≤2）}\end{array}\right.$．

点评 本题是四边形的综合题，考查了矩形的性质、折叠的性质、三角形全等的性质和判定、特殊角的三角函数值、直角三角形30度的性质、三角形面积，且利用分类讨论的思想解决第三问的面积问题．