
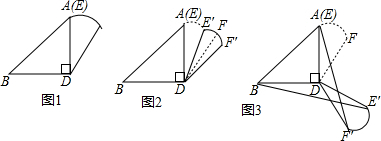
分析 (1)先利用直角三角形的性质,求出∠BAD,再由平行得到∠ADF′即可;
(2)先求出∠ADF′,再判断△ADF′≌△BDE′即可.
解答 解:(1)∵∠ADB=90°,DA=DB,
∴∠BAD=45°,
∵DF′∥AB,
∴∠ADF′=∠BAD=45°,
∴α=45°-30°=15°,
(2)∵α=120°,
∴∠ADE′=120°,
∴∠ADF′=120°+30°=150°,
∠BDE′=360°-90°-120°=150°,
∴∠ADF′=∠BDE′,
在△ADF′和△BDE′中,
$\left\{\begin{array}{l}{DA=DB}\\{∠ADF′=∠BDE′}\\{DE′=DF′}\end{array}\right.$,
∴△ADF′≌△BDE′,
∴AF′=BE′.
点评 此题是旋转性质题,主要考查了旋转角,全等三角形的判定和性质,解本题的关键是旋转角的计算.


科目:初中数学 来源: 题型:选择题
| A. | 同位角一定不相等 | B. | 内错角的对顶角-定相等 | ||
| C. | 同位角的邻补角一定相等 | D. | 两对同旁内角的和一定大于180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由4x-6=2x+3移项得4x+2x=3-6 | |
| B. | 由$\frac{4}{7}x=5-\frac{x-1}{7}$,去分母得4x=5-x-1 | |
| C. | 由2(x+3)-3(x-1)=7,去括号得 2x+3-3x+1=7 | |
| D. | 由$\frac{x}{0.3}-0.5=x$得 $\frac{10x}{3}-\frac{1}{2}=x$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根 | |
| B. | 如果方程M有两根符号相同,那么方程N的两根符号也相同 | |
| C. | 如果5是方程M的一个根,那么$\frac{1}{5}$是方程N的一个根 | |
| D. | 如果方程M和方程N有一个相同的根,那么这个根必是x=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
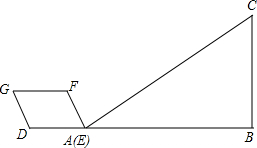 平行四边形DEFG和Rt△ABC如图放置在同一直线上,点E与点A重合,AB=9,DE=3,DG=2,∠G=∠C=60°,∠B=90°.平行四边形DEFG从如图所示状态开始向右沿AB方向以每秒1个单位的速度平移,设运动的时间为t,直到点E与点B重合为止:
平行四边形DEFG和Rt△ABC如图放置在同一直线上,点E与点A重合,AB=9,DE=3,DG=2,∠G=∠C=60°,∠B=90°.平行四边形DEFG从如图所示状态开始向右沿AB方向以每秒1个单位的速度平移,设运动的时间为t,直到点E与点B重合为止:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读下面材料:在数学课上,老师提出如下问题:尺规作图:
阅读下面材料:在数学课上,老师提出如下问题:尺规作图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com