
【题目】如图,一艘巡逻艇航行至海面B处时,得知正北方向上距B处20海里的C处有一渔船发生故障,就立即指挥港口A处的救援艇前往C处营救.已知C处位于A处的北偏东45°的方向上,港口A位于B的北偏西30°的方向上.求A、C之间的距离.(结果精确到0.1海里,参考数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)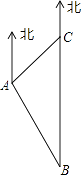
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知如图,四边形ABCD的四个顶点的坐标分别为A(0,0)、B(9,0)、C(7,5)、D(2,7).
(1)试计算四边形ABCD的面积;
(2)若将该四边形各顶点的横坐标都加2,纵坐标都加3,其面积怎么变化?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬“敬老爱老”传统美德,某校八年级(1)班的学生要去距离学校10km的敬老院看望老人,一部分学生骑自行车先走,过了20min后,其余学生乘汽车出发,结果乘汽车的同学早到10min.已知汽车的速度是骑车学生的4倍,求骑车学生的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4>kx+b的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在城镇化建设中,开发商要处理A地大量的建筑垃圾,A地只能容纳1台装卸机作业,装卸机平均每6分钟可以给工程车装满一车建筑垃圾,每辆工程车要将建筑垃圾运送至20千米的B处倾倒,每次倾倒时间约为1分钟,倾倒后立即返回A地等候下一次装运,直到装运完毕;工程车的平均速度为40千米/时.
(1)一辆工程车运送一趟建筑垃圾(从装车到返回)需要多少分钟?
(2)至少安排多少辆工程车既能保证装卸机不空闲,又能保证工程车最少等候时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化妆品店老板到厂家选购A、B两种品牌的化妆品,若购进A品牌的化妆品5套,B品牌的化妆品6套,需要950元;若购进A品牌的化妆品3套,B品牌的化妆品2套,需要450元.
![]() 求A、B两种品牌的化妆品每套进价分别为多少元?
求A、B两种品牌的化妆品每套进价分别为多少元?
![]() 若销售1套A品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套,且B品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货?
若销售1套A品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套,且B品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 ( )
①2∠DCF=∠BCD; ②EF=CF; ③S△BEC=2S△CEF; ④∠DFE=3∠AEF.

A. ①②③④ B. ①②④ C. ①② D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑公司开发出一种软件,从研发到年初上市后,经历了从亏损到盈利的过程,如图中的图象是抛物线的一段,它刻画了该软件上市以来累积利润S(万元)与销售时间t(月)之间的函数关系(即前t个月的利润总和S与t之间的函数关系),根据图象提供的信息,解答下列问题: 
(1)该种软件上市第几个月后开始盈利?
(2)求累积利润S(万元)与时间t(月)之间的函数表达式;
(3)截止到几月末,公司累积利润达到30万元?
(4)求公司第6个月末所累积的利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com