
分析 (1)先去小括号、再去中括号后移项,然后合并得到-5x=-11,然后把x的系数化为1即可;
(2)先去分母,再去括号后移项,然后合并得到2x=-76,然后把x的系数化为1即可.
解答 解:(1)$\frac{1}{2}$(x-$\frac{1}{2}$x+$\frac{1}{2}$)=$\frac{2}{3}$x-$\frac{2}{3}$,
$\frac{1}{2}$($\frac{1}{2}$x+$\frac{1}{2}$)=$\frac{2}{3}$x-$\frac{2}{3}$,
$\frac{1}{4}$x+$\frac{1}{4}$=$\frac{2}{3}$x-$\frac{2}{3}$,
3x+3=8x-8,
3x-8x=-8-3,
-5x=-11,
所以x=$\frac{11}{5}$;
(2)15x-3(x-2)=5(2x-5)-45,
15x-3x+6=10x-25-45,
15x-3x-10x=-25-45-6,
2x=-76,
所以x=-38.
点评 本题考查了解一元一次方程:去分母、去括号、移项、合并同类项、系数化为1,这仅是解一元一次方程的一般步骤,针对方程的特点,灵活应用,各种步骤都是为使方程逐渐向x=a形式转化.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
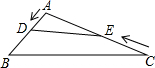 如图,在钝角△ABC中,AB=3cm,AC=6cm,动点D从点A出发到点B止.动点E从点C出发到点A止.点D运动的速度为1cm/s,点E运动的速度为3cm/s.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时.运动的时间是$\frac{6}{5}$秒或$\frac{12}{7}$秒.
如图,在钝角△ABC中,AB=3cm,AC=6cm,动点D从点A出发到点B止.动点E从点C出发到点A止.点D运动的速度为1cm/s,点E运动的速度为3cm/s.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时.运动的时间是$\frac{6}{5}$秒或$\frac{12}{7}$秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com