
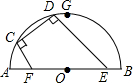
 如图,AB为半圆所在⊙O的直径,弦CD为定长且小于⊙O的半径(C点与A点不重合),CF⊥CD交AB于点F,DE⊥CD交AB于点E,G为半圆弧上的中点.当点C在$\widehat{AG}$上运动时,设$\widehat{AG}$的长为x,CF+DE=y.则下列图象中,能表示y与x的函数关系的图象大致是( )
如图,AB为半圆所在⊙O的直径,弦CD为定长且小于⊙O的半径(C点与A点不重合),CF⊥CD交AB于点F,DE⊥CD交AB于点E,G为半圆弧上的中点.当点C在$\widehat{AG}$上运动时,设$\widehat{AG}$的长为x,CF+DE=y.则下列图象中,能表示y与x的函数关系的图象大致是( )| A. | 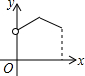 | B. | 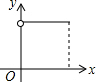 | C. |  | D. | 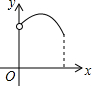 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | $\frac{11}{3}$ | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
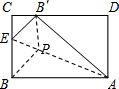 如图所示,矩形纸片ABCD中,AB=5,AD=4,将纸片折叠,使点D落在边CB上的D′处,折痕为AE,在折痕AE上存在一点P到边CB的距离与到点D的距离相等,则此相等距离为2.5.
如图所示,矩形纸片ABCD中,AB=5,AD=4,将纸片折叠,使点D落在边CB上的D′处,折痕为AE,在折痕AE上存在一点P到边CB的距离与到点D的距离相等,则此相等距离为2.5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:| 收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
| A | 7 | 25 | 0.01 |
| B | m | n | 0.01 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
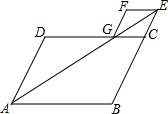 如图,在平行四边形ABCD中,∠BAD的平分线交BC的延长线于点E,交CD于点G,过点E作EF∥CD,过点G作FG∥EC,EF,FG交于点F.求证:四边形CEFG为菱形.
如图,在平行四边形ABCD中,∠BAD的平分线交BC的延长线于点E,交CD于点G,过点E作EF∥CD,过点G作FG∥EC,EF,FG交于点F.求证:四边形CEFG为菱形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}×\sqrt{3}=\sqrt{6}$ | B. | $\sqrt{8}÷\sqrt{2}=2$ | C. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | D. | ${(-\sqrt{3})^2}=3$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com