
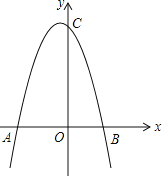
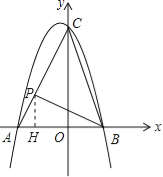
【题目】如图,抛物线y=﹣x2﹣x+6与x轴交于A、B两点,与y轴交于点C.
(1)求点A、B的坐标;
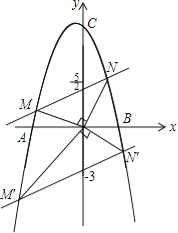
(2)设点P是线段AC上一点,且S△ABP:S△BCP=1:3,求点P的坐标;
(3)若直线y=![]() x+a与抛物线交于M、N两点,当∠MON为锐角时,求a的取值范围.
x+a与抛物线交于M、N两点,当∠MON为锐角时,求a的取值范围.
【答案】(1)A(﹣3,0),B(2,0);(2)P(﹣![]() ,
, ![]() );(3)a<﹣3或
);(3)a<﹣3或![]() <a<
<a<![]()
【解析】试题分析:(1)将y=0代入y=-x2-x+6,得出-x2-x+6=0,解方程求得x1=-3,x2=2,即可得到点A、B的坐标;
(2)先由抛物线y=-x2-x+6与y轴交于点C,得出OC=6.根据同高的两个三角形面积比等于底边之比,得到![]() ,过P作PH⊥x轴,垂足为H,那么
,过P作PH⊥x轴,垂足为H,那么![]() .由PH∥CO,根据平行线分线段成比例定理求得PH=
.由PH∥CO,根据平行线分线段成比例定理求得PH=![]() ,AH=
,AH=![]() ,那么HO=
,那么HO=![]() ,进而得到点P的坐标;
,进而得到点P的坐标;
(3)设直线y=![]() x+a与抛物线y=-x2-x+6交于M(x1,y1)、N(x2,y2)两点(M在N的左侧),由
x+a与抛物线y=-x2-x+6交于M(x1,y1)、N(x2,y2)两点(M在N的左侧),由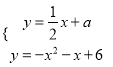 ,得x2+
,得x2+![]() x+a-6=0,根据一元二次方程根与系数的关系得出x1+x2=-
x+a-6=0,根据一元二次方程根与系数的关系得出x1+x2=-![]() ,x1x2=a-6,由y1=
,x1x2=a-6,由y1=![]() x1+a,y2=
x1+a,y2=![]() x2+a,得到y1y2=(
x2+a,得到y1y2=(![]() x1+a)(
x1+a)(![]() x2+a)=
x2+a)=![]() -
-![]() a+a2.当∠MON=90°时,由勾股定理得到OM2+O2=MN2,即
a+a2.当∠MON=90°时,由勾股定理得到OM2+O2=MN2,即![]() =(x2-x1)2+(y2-y1)2,化简整理得出x1x2+y1y2=0,依此求出a=-3或a=
=(x2-x1)2+(y2-y1)2,化简整理得出x1x2+y1y2=0,依此求出a=-3或a=![]() .再求出抛物线与直线只有一个公共点时,a=
.再求出抛物线与直线只有一个公共点时,a=![]() .然后结合图形可知把直线y=
.然后结合图形可知把直线y=![]() x-3向下平移,∠MON是锐角;把直线y=
x-3向下平移,∠MON是锐角;把直线y=![]() x+
x+![]() 向上平移,∠MON也是锐角,进而求出a的取值范围.
向上平移,∠MON也是锐角,进而求出a的取值范围.
试题解析:(1)∵y=-x2-x+6,
∴y=0时,即-x2-x+6=0,解得x1=-3,x2=2,
∴A(-3,0),B(2,0);
(2)令x=0,得y=6,即OC=6.
由于△ABP和△BCP的高相等,所以面积比等于底边之比,
即![]() ,
,
过P作PH⊥x轴,垂足为H, ![]() .
.
∵PH∥CO,
∴![]() ,
,
∴PH=![]() ,AH=
,AH=![]() ,
,
∴HO=![]() ,
,
∴P(-![]() ,
, ![]() );
);
(3)设直线y=![]() x+a与抛物线y=-x2-x+6交于M(x1,y1)、N(x2,y2)两点(M在N的左侧),
x+a与抛物线y=-x2-x+6交于M(x1,y1)、N(x2,y2)两点(M在N的左侧),
由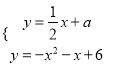 ,得x2+
,得x2+![]() x+a-6=0,
x+a-6=0,
则x1+x2=-![]() ,x1x2=a-6,
,x1x2=a-6,
∵y1=![]() x1+a,y2=
x1+a,y2=![]() x2+a,
x2+a,
∴y1y2=(![]() x1+a)(
x1+a)(![]() x2+a)
x2+a)
=![]() x1x2+
x1x2+![]() (x1+x2)a+a2
(x1+x2)a+a2
=![]() -
-![]() a+a2.
a+a2.
当∠MON=90°时,OM2+ON2=MN2,
即![]() =(x2-x1)2+(y2-y1)2,
=(x2-x1)2+(y2-y1)2,
∴x1x2+y1y2=0,
∴a-6+![]() -
-![]() a+a2=0,即a2+
a+a2=0,即a2+![]() a-
a-![]() =0,
=0,
∴a=-3或a=![]() .
.
若抛物线与直线只有一个公共点,即方程x2+![]() x+a-6=0有两个相等的实数根,
x+a-6=0有两个相等的实数根,
则△=b2-4ac=0,解得:a=![]() .
.
把直线y=![]() x-3向下平移,∠MON是锐角,此时a<-3,
x-3向下平移,∠MON是锐角,此时a<-3,
把直线y=![]() x+
x+![]() 向上平移,∠MON也是锐角,此时
向上平移,∠MON也是锐角,此时![]() <a<
<a<![]() .
.
综上所述,a的取值范围是a<-3或![]() <a<
<a<![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+2(a≠0)的图象与x 轴交于A,B 两点,与y 轴交于点C,已知点 A(-4,0),B(1,0).
(1)求抛物线的解析式;
(2)若点 D(m,n) 是抛物线在第二象限的部分上的一动点,四边形 ![]() 的面积为
的面积为 ![]() ,求
,求 ![]() 关于 m 的函数关系;
关于 m 的函数关系;
(3)若点 E 为抛物线对称轴上任意一点,当以 A,C,E 为顶点的三角形是直角三角形时,请求出满足条件的所有点 E 的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察如图所示的长方体后填空
用符号表示下列两棱的位置关系:
A1B1____AB ,AA1____AB ,
A1D1____C1D1 , AD____BC;
(2)A1B1与BC所在的直线是两条不相交的直线,他们_ ___平行线(填“是”或“不是”).由此可知,在__________,两条不相交的直线才能叫平行线.
(3)在同一平面内,两条不重合的直线位置关系只有_____种,即_____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com