
【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=30°,点D在△ABC外,且BD=2.连AD、CD,则△ACD的周长最小值为( )

A. 1B. ![]() C. 2D. 2
C. 2D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某一城市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天,乙队单独完成这项工程需要90天;若由甲队先做20天,剩下的工程由甲、乙两队合做完成.
(1)甲、乙两队合作多少天?
(2)甲队施工一天需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
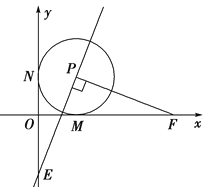
【题目】已知O是坐标原点,以P(1,1)为圆心的⊙P与x轴、y轴分别相切于点M和点N.点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连结PF,过点P作PE⊥PF交y轴于点E.设点F运动的时间是t秒(t>0).
(1)求点E的坐标(用t表示);
(2)在点F运动过程中,当PF=2OE时,求t的值.
(3)当t>1时,作点F关于点M的对称点F′.点Q是线段MF′的中点,连结QE.在点F运动过程中,是否存在某一时刻,使得△QOE与△PMF相似,若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.某酒厂生产A,B两种品牌的酒,平均每天两种酒共可售出600瓶,每种酒每瓶的成本和售价如表所示,设平均每天共获利y元,平均每天售出A种品牌的酒x瓶.
A | B | |
成本(元) | 50 | 35 |
售价(元) | 70 | 50 |
(1)请写出y关于x的函数关系式;
(2)如果该厂每天至少投入成本25000元,且售出的B种品牌的酒不少于全天销售总量的55%,那么共有几种销售方案?并求出每天至少获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地建设一项水利工程,工程需要运送的土石方总量为360万米3.
(1)写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万米3)之间的函数关系式;
(2)当运输公司平均每天的工作量15万米3,完成任务所需的时间是多少?
(3)为了能在150天内完成任务,平均每天的工作量至少是多少万米3?
查看答案和解析>>
科目:初中数学 来源: 题型:
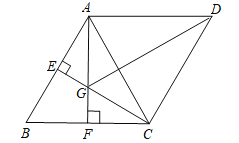
【题目】如图,在平行四边形ABCD中,E、F分别是AB、BC的中点,CE⊥AB,垂足为E,AF⊥BC,垂足为F,AF与CE相交于点G.
(1)证明:△CFG≌△AEG.
(2)若AB=4,求四边形AGCD的对角线GD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com