
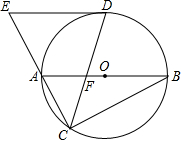
 如图,⊙O是△ABC的外接圆,AB为⊙O的直径,∠ACB的平分线交⊙O于点D,交AB于点F;过D作⊙O的切线,交CA延长线于点E.
如图,⊙O是△ABC的外接圆,AB为⊙O的直径,∠ACB的平分线交⊙O于点D,交AB于点F;过D作⊙O的切线,交CA延长线于点E.分析 (1)连接BD.根据直径所对的圆周角是90°,可知:∠ACB=90°,从而可求得∠ABD=∠ACD=∠DCB=45°由弦切角定理可知:∠CDE=∠CBA+45°,由三角形外角的性质可知∠CFA=∠CBA+45°,故此∠AFC=∠EDC,从而可证明AB∥ED,
(2)先根据角平分线的性质定理得出DG=DM,CM=CG,进而得出CG=$\frac{\sqrt{2}}{2}$CD再判断出Rt△ADG≌Rt△BDM,最后等量代换即可;
(3)先根据三角函数得出BC=2x,AB=$\sqrt{5}$x,再用角平分线定理得出AF和BF,借助(2)结论得出CF,CD,进而用相交弦定理建立方程求出x,最后用平行线分线段成比例定理得出DE.
解答 解:(1)如图1,
∵AB是圆O的直径,
∴∠ACB=90°.
∵CD平分∠ACB,
∴∠ACD=∠DCB=45°.
∴∠ABD=∠ACD=45°.
由弦切角定理可知:∠CDE=∠CBD=∠CBA+∠ABD=∠CBA+45°.
∵∠CFA=∠FCB+∠CBA=∠CBA+45°,
∴∠AFC=∠EDC.
∴AB∥ED,
(2)AC+BC=$\sqrt{2}$CD
理由:如图2,
连接BD,AD,过点D作DG⊥AC,DM⊥BM,
∵∠ACD=∠BCD,
∴DG=DM,CM=CG
由(1)知,AB∥DE,且DE是⊙O的切线,
∴点D是半圆的中点,
∵AB是直径,
∴AD=BD,
在Rt△ADG和Rt△BDM中,$\left\{\begin{array}{l}{AD=BD}\\{DG=DM}\end{array}\right.$,
∴Rt△ADG≌Rt△BDM,
∴AG=BM,
在Rt△CDG中,∠DCG=45°,
∴CD=$\sqrt{2}$CG,
∴CG=$\frac{\sqrt{2}}{2}$CD
∴AC+BC=AC+CM+BM=AC+CM+AG=CM+CG=2CG=$\sqrt{2}$CD;
即:AC+BC=$\sqrt{2}$CD
故答案为:AC+BC=$\sqrt{2}$CD
(3)设AC=x,
∵tan∠B=$\frac{1}{2}$=$\frac{AC}{BC}$,
∴BC=2x,
∴AB=$\sqrt{5}$x,
∵CD平分∠ACB,
∴$\frac{AF}{BF}=\frac{AC}{BC}$=$\frac{1}{2}$,
∴AF=$\frac{\sqrt{5}}{3}$x,BF=$\frac{2\sqrt{5}}{3}$x,
由(2)知,$\sqrt{2}$CD=AC+BC=3x,
∴CD=$\frac{3\sqrt{2}}{2}$x,
∵DF=5$\sqrt{2}$,
∴CF=CD-DF=$\frac{3\sqrt{2}}{2}$x-5$\sqrt{2}$,
根据相交弦定理得,DF×CF=AF×BF,
∴5$\sqrt{2}$($\frac{3\sqrt{2}}{2}$x-5$\sqrt{2}$)=$\frac{\sqrt{5}}{3}$x•$\frac{2\sqrt{5}}{3}$x,
∴x=6或x=$\frac{15}{2}$,
当x=6时,AF=2$\sqrt{5}$,BF=4$\sqrt{5}$,CD=9$\sqrt{2}$,CF=4$\sqrt{2}$,
∵AB∥DE,
∴$\frac{AF}{DE}=\frac{CF}{CD}$,
∴$\frac{2\sqrt{5}}{DE}=\frac{4\sqrt{2}}{9\sqrt{2}}$,
∴DE=$\frac{9\sqrt{5}}{2}$,
当x=$\frac{15}{2}$,AF=$\frac{5\sqrt{5}}{2}$,CF=$\frac{25\sqrt{2}}{4}$,CD=$\frac{45\sqrt{2}}{2}$,
∵AB∥DE,
∴$\frac{AF}{DE}=\frac{CF}{CD}$,
∴$\frac{\frac{5\sqrt{5}}{2}}{DE}=\frac{\frac{25\sqrt{2}}{4}}{\frac{45\sqrt{2}}{2}}$,
∴DE=$\frac{{9\sqrt{5}}}{2}$.
即:DE的长为$\frac{{9\sqrt{5}}}{2}$.
点评 此题是圆的综合题,主要考查了角平分线的性质,切线的性质,平行线的判定,全等三角形的判定和性质,相交弦定理,解本题的关键是构造出全等三角形,难点是求出DE,是一道中等难度的中考常考题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中模拟数学试卷(解析版) 题型:解答题
计算:
(1)|-1|+(—2)3+(7-π)0-( )-1;
)-1;
(2) (-2a)3·(a2)2÷a3
(3) (3a+b-2)(3a-b+2)
(4)10002-1002×998
(5) (x+1)(x2+1)(x4+1)(x-1)
(6) (3a+2)2(3a-2)2
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
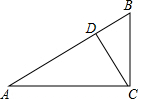 如图,在Rt△ABC中,CD是斜边AB上的高,∠A≠45°,则下列比值中不等于sinA的是( )
如图,在Rt△ABC中,CD是斜边AB上的高,∠A≠45°,则下列比值中不等于sinA的是( )| A. | $\frac{CD}{AC}$ | B. | $\frac{CB}{AB}$ | C. | $\frac{BD}{CB}$ | D. | $\frac{CD}{CB}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
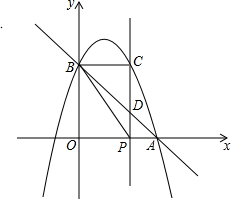 如图,已知抛物线y=-x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),点P是x轴上一动点,过点P作x轴的垂线交抛物线于点C,交直线AB于点D,设P(x,0).
如图,已知抛物线y=-x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),点P是x轴上一动点,过点P作x轴的垂线交抛物线于点C,交直线AB于点D,设P(x,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
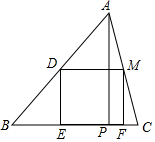 如图,△ABC是一块面积为2700cm2的三角形木板,其中BC=90cm,现在要将这块木板加工成一个正方形的桌面,如图所示,正方形DEFM即是要加工成的桌面,点D、M分别在AB、AC边上,点E、F在BC边上,根据以上数据求出这个正方形桌面的边长.
如图,△ABC是一块面积为2700cm2的三角形木板,其中BC=90cm,现在要将这块木板加工成一个正方形的桌面,如图所示,正方形DEFM即是要加工成的桌面,点D、M分别在AB、AC边上,点E、F在BC边上,根据以上数据求出这个正方形桌面的边长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
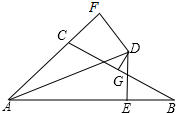 如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=10cm,AC=6cm,则BE的长为2cm.
如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=10cm,AC=6cm,则BE的长为2cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com