
分析 先求出方程①②的解,从而得到关于a的方程,然后解方程求出a的值.
解答 解:4(x-3)+2a=-x+5…①;
去括号得:4x-12+2a=-x+5,
移項、合并同类項得:5x=17-2a,
系数化为1得:x=$\frac{17-2a}{5}$
7x-3=a+x…②,
移項得:6x=a+3,
方程两边都乘以6得,x=$\frac{a+3}{6}$,
∵方程①与方程②的根的比为6:5,
∴$\frac{\frac{17-2a}{5}}{\frac{a+3}{6}}$=$\frac{6}{5}$,
整理得,17-2a=a+3,
解得a=$\frac{14}{3}$.
点评 本题考查了一元一次方程的解,熟练掌握方程得解就是使方程的左右两边相等的未知数的值是解题的关键.


科目:初中数学 来源: 题型:解答题
 平面直角坐标系中,点A在函数y1=$\frac{2}{x}$(x>0)的图象上,点B在y2=-$\frac{2}{x}$(x<0)的图象上,设A的横坐标为a,B的横坐标为b.
平面直角坐标系中,点A在函数y1=$\frac{2}{x}$(x>0)的图象上,点B在y2=-$\frac{2}{x}$(x<0)的图象上,设A的横坐标为a,B的横坐标为b.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
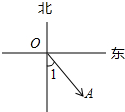 如图,O为我国南海某人造海岛,某国商船在A的位置,∠1=40°,下列说法正确的是( )
如图,O为我国南海某人造海岛,某国商船在A的位置,∠1=40°,下列说法正确的是( )| A. | 商船在海岛的北偏西50°方向 | B. | 海岛在商船的北偏西40°方向 | ||
| C. | 海岛在商船的东偏南50°方向 | D. | 商船在海岛的东偏南40°方向 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知:如图,AE平分∠BAD,BD平分∠ABE,且∠BAD+∠ABE=180°,求∠1与∠2的关系
已知:如图,AE平分∠BAD,BD平分∠ABE,且∠BAD+∠ABE=180°,求∠1与∠2的关系查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com