
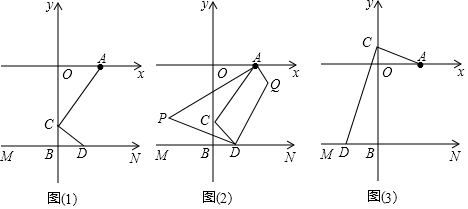
���� ��1������CD��CA����AOC=90��֪��DCB=��OAC���ɡ�CBD=90��ɵá�DCB+��CDB=90�㣬����CAO+��CDB=90�㣻
��2���ӳ�AP��MN�ڵ�E����ϣ�1���н��ۣ����ý�ƽ���߿ɵá�1+��2=45�㣬����ƽ���ߵ����ʺ�������������ʿɵã�
��3����APƽ�֡�OAC��AQƽ�֡�CAx�ҡ�OAC+��CAx=180��ɵá�PAQ=90�㣬ͬ��֪��PDQ=90�㣬�����ı����ڽǺͿɵý��ۣ�
��4�����CAQ=2������CQA=2�£��ɡ�ACD=90���2��+2��=90�㼴��+��=45�㣬���ݽ�ƽ���ߵ����ʼ�ƽ�������ʿɵá�QDP=�£�$��CAQ=\frac{1}{2}$��CAQ=�����ɡ�CQA=90��-������������ʿɵô𰸣�
��� �⣺��1����ͼ����CD��CA��
���ACO+��DCB=90�㣬
�ߡ�AOC=90�㣬
���ACO+��OAC=90�㣬
���DCB=��OAC��
�֡ߡ�CBD=90�㣬
���DCB+��CDB=90�㣬
���CAO+��CDB=90�㣻
��2����ͼ2���ӳ�AP��MN�ڵ�E��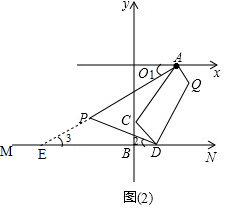
��APƽ�֡�CAO��DPƽ�֡�CDB��
���1=$\frac{1}{2}$��CAO����2=$\frac{1}{2}$��CDB��
�ߡ�CAO+��CDB=90�㣬
���1+��2=45�㣬
��MN��OA��
���1=��3��
���APD=��2+��3=��1+��3=45�㣻
��3����APƽ�֡�OAC��AQƽ�֡�CAx��
���PAC=$\frac{1}{2}$��OAC����QAC=$\frac{1}{2}$��CAx��
�ߡ�OAC+��CAx=180�㣬
���PAQ=��PAC+��CAQ=$\frac{1}{2}$����OAC+��CAx��=90�㣬
ͬ���á�PDQ=90�㣬
���APD+��AQD=360��-����PAQ+��PDQ��=180�㣻
��4����APD�Ĵ�С���䣬Ϊ45�㣻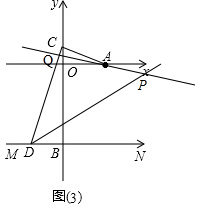
���CAQ=2������CQA=2�£�
�ߡ�ACD=90�㣬
���CAQ+��CQA=90�㣬��2��+2��=90����+��=45��
��AO��MN��
���CQA=��CDB=2�£�
��AQƽ�֡�CAQ��DBƽ�֡�CDB��
���QDP=$\frac{1}{2}$��CDB=�£�$��CAQ=\frac{1}{2}$��CAQ=����
���CQA=90��-��CAQ=90��-����
���APD=��CQA-��CDB=90��-��-��=45�㣮
���� ������Ҫ�����ƽ���ߵ����ʡ�������������ʡ�ƽ���ߵ����ʵ�֪ʶ�㣬�������ս�ƽ���ߵ����ʡ���������������ǽ���Ĺؼ���


 �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����?ABCD�У���E��F�ֱ���BC��AD�ϵĵ㣬��BE=DF���Խ���AC��AB��
��ͼ����?ABCD�У���E��F�ֱ���BC��AD�ϵĵ㣬��BE=DF���Խ���AC��AB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 Ϊ���γ��нֵ����������������������ij�ֵ��Խ������������٣���ͼ��һ��С������ij���нֵ���ֱ�У�ijһʱ�̸պ���ʻ���복�ټ����A60m��C��������4s��С���������복�ټ����A100m��B������֪�öγ��нֵ�������Ϊ60km/h����������С�����Ƿ��٣�
Ϊ���γ��нֵ����������������������ij�ֵ��Խ������������٣���ͼ��һ��С������ij���нֵ���ֱ�У�ijһʱ�̸պ���ʻ���복�ټ����A60m��C��������4s��С���������복�ټ����A100m��B������֪�öγ��нֵ�������Ϊ60km/h����������С�����Ƿ��٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | Ͷ��һö���ȵ�Ӳ��100�Σ����泯�ϵĴ���Ϊ50�� | |
| B�� | ����һ��һԪ���η��̶���ʵ���� | |
| C�� | �����ε������������ε��ⲿ | |
| D�� | ֱ�������ε���б���ϵ����ߵ���б�ߵ�һ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com