
����Ŀ��ij�д�������ɫ��չģ������������Ծ��ڳ�����������Ҫ��ȾԴ��������ˮ���ؽ�������Ⱦ���ŷţ��ֱ�����������ˮ���д��������³Ƽ����������ؽ�����ת�����������³��ҷ�������������������ˮ��Ⱦָ����ΪQ���ؽ��������ҷ�������һ���������������깤�����ӵ��꿪ʼ����������ÿ�ҹ���һ�꽵�͵�Qֵ����ƽ��ֵn���㣮��һ����40�ҹ������ҷ�����������ʹQֵ������12�������������������ڳ���ˮ�����Ը��ƣ�
��1����n��ֵ��
��2���ӵڶ�����ÿ�����ҷ����������Ĺ�����������һ�궼������ͬ�İٷ���m�����������ҷ��������Ĺ���������190�ң���m��ֵ��������ڶ������ҷ����������Ĺ���������
��3������������ˮ�ü����������ӵڶ�����ÿ����˽��͵�Qֵ����һ�궼���Ӹ���ͬ����ֵa���ڣ�2��������£��ڶ��꣬���ҷ����������Ĺ����ϼƽ��͵�Qֵ�뵱��������������͵�Qֵ��ȣ������꣬�ü���ʹQֵ������39.5�����һ���ü����������͵�Qֵ��a��ֵ��
���𰸡���1��0.3����2��60�ң���3��Q=20.5��a=9.5.
��������
��1��ֱ�����õ�һ����40�ҹ������ҷ�����������ʹQֵ������12���ó���ʽ����𰸣�
��2�����ôӵڶ�����ÿ�����ҷ����������Ĺ�����������һ�궼������ͬ�İٷ���m�����������ҷ��������Ĺ���������190�ҵó���ʽ����𰸣�
��3������n��ֵ���ɵó�����a�ĵ�ʽ����𰸣�
��1��������ɵã�40n=12��
��ã�n=0.3��
��2��������ɵã�40+40��1+m��+40��1+m��2=190��
��ã�m1=![]() ��m2=��
��m2=��![]() ����ȥ����
����ȥ����
��ڶ������ҷ����������Ĺ�������Ϊ��40��1+m��=40��1+50%��=60���ң���
��3�����һ�����ҷ�������������100n=100��0.3=30��
��30��a��+2a=39.5��
��ã�a=9.5��
��Q=20.5��
���һ���ü����������͵�QֵΪx��
�ڶ���Qֵ���ҷ�������������100n=100��0.3=30��
�ⷨһ����30��a��+2a=39.5
a=9.5
x=20.5


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��23����-5��-��-3����![]() ��
��
��2����-3����![]() +8����-2
+8����-2![]() ��-11����-
��-11����-![]() ����
����
��3����-1��2-��-1![]() ������-24����
������-24����
��4��![]() ��-2��2-��
��-2��2-��![]() ��3+[1+��-
��3+[1+��-![]() ��2����-1
��2����-1![]() ��]��
��]��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
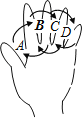
����Ŀ����ͼΪ�ֵ�ʾ��ͼ���ڸ�����ָ������ĸA��B��C��D�����㰴ͼ�м�ͷ��ָ����A��B��C��D��C��B��A��B��C�����ķ�ʽ����A��ʼ ��������������1��2��3��4����������12ʱ����Ӧ����ĸ��_____������ĸC��201�γ���ʱ��ǡ������������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=![]() x2+
x2+![]() x��
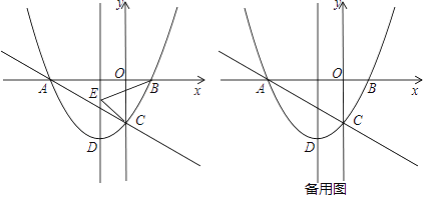
x��![]() ��ͼ����x�ύ�ڵ� A��B���� y ���ڵ� C�������ߵĶ���Ϊ D��
��ͼ����x�ύ�ڵ� A��B���� y ���ڵ� C�������ߵĶ���Ϊ D��
��1���������߶��� D �������Լ�ֱ�� AC �ĺ�������ʽ��
��2���� P ����������һ�㣬�ҵ�P��ֱ�� AC �·����� E �������߶Գ����ϣ�����BCE ���ܳ���Сʱ������PCE ��������ֵ�Լ���ʱ�� P �����ꣻ
��3���ڣ�2���������£����� P ��ƽ���� AC ��ֱ�߷ֱ�x���ڵ� M���� y ���ڵ�N����������y=![]() x2+
x2+![]() x��
x��![]() �ضԳ�������ƽ�ƣ�ƽ�ƺ������ߵĶ���Ϊ D'����ƽ�ƵĹ����У��Ƿ���ڵ� D'��ʹ�õ� D'��M��N ���㹹�ɵ�������Ϊֱ�������Σ������ڣ�ֱ��д���� D'�����ꣻ�������ڣ���˵�����ɣ�
�ضԳ�������ƽ�ƣ�ƽ�ƺ������ߵĶ���Ϊ D'����ƽ�ƵĹ����У��Ƿ���ڵ� D'��ʹ�õ� D'��M��N ���㹹�ɵ�������Ϊֱ�������Σ������ڣ�ֱ��д���� D'�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���»��̳�����ij�ֱ��䣬ÿ̨������Ϊ2500Ԫ���г����б����������ۼ�Ϊ2900Ԫʱ��ƽ��ÿ�����۳�8̨���������ۼ�ÿ����50Ԫʱ��ƽ��ÿ����ܶ��۳�4̨���̳�Ҫ��ʹ���ֱ������������ƽ��ÿ��ﵽ5000Ԫ����ÿ̨����Ķ���ΪxԪ����x����Ĺ�ϵʽΪ�� ��
A. (x2500)(8+4��![]() )=5000 B. (2900x2500)(8+4��
)=5000 B. (2900x2500)(8+4��![]() )=5000
)=5000
C. (x2500)(8+4��![]() )=5000 D. (2900x)(8+4��
)=5000 D. (2900x)(8+4��![]() )=5000
)=5000
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ����ﴫͳ�Ļ�����������У����У�ѧУ�ƻ���չ��������A����ѧ�ж�������B���ݽ�������C���α��硱����D���鷨����Ҫ��ÿλͬѧ������ֻ�ܲμ�����һ����ѧУΪ���˽�ѧ������Ը����������˲���ѧ�������ͳ�����£�
��1����ͼ��ϣ���μӻCռ20%��ϣ���μӻBռ15%�������������Ϊ �ˣ�����ͳ��ͼ�У�ϣ���μӻD��ռԲ�Ľ�Ϊ �ȣ�����������Ϣ��ȫ����ͳ��ͼ��
��2��ѧУ����800��ѧ���������ͼ����Ϣ������ȫУѧ��ϣ���μӻA�ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���![]() �У��Խ���
�У��Խ���![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() ��
��![]() �ֱ��ǶԽ���BD�ϵ����㣬���������ĸ���������
�ֱ��ǶԽ���BD�ϵ����㣬���������ĸ���������![]() ����
����![]() ����
����![]() ����
����![]() .�������ж��ı���
.�������ж��ı���![]() ��ƽ���ı��εĸ�����
��ƽ���ı��εĸ�����

A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��B�������϶�Ӧ�����ֱ���![]() ��
��![]() ��ʾ����
��ʾ����![]() .
.
��1�������ϵ�A��ʾ�������� ������B��ʾ��������
��2����һ����P�ӵ�A��������3����λ���ȣ����ٶ���A��B�˶�������Q��ԭ��O��������1����λ���ȣ����ٶ���B�˶�����P��Qͬʱ��������Q�˶���B��ʱ����ͬʱֹͣ.���Q�˶�ʱ��Ϊt��.
����P��A��B�˶�����P���ʾ����Ϊ ,Q���ʾ����Ϊ .�ú�![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
�ڵ�tΪ��ֵʱ����P���Q֮��ľ���Ϊ2����λ���ȣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ��κ���![]() ��������˵����
��������˵����
�������x��1ʱ![]() ��
��![]() �������������m��1��
�������������m��1��
���������ͼ����x���������ľ�����4����![]() ��
��
�����������ͼ������ƽ��3����λ���ĺ�������Сֵ��-4����m=��1��
�������x=1ʱ�ĺ���ֵ��x=2013ʱ�ĺ���ֵ�������x=2014ʱ�ĺ���ֵΪ��3��
������ȷ��˵���� ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com