
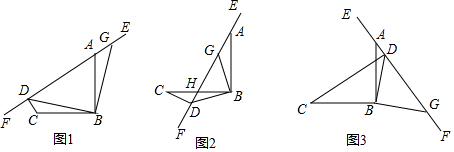
���� ��1�����ݡ�ABC=90�㣬GB��DB���á�ABD+��DBC=90�㣬��ABD+��GBA=90�㣬��DBC=��GBA�����ı��ε��ڽǺͣ��á�DAB+��DBC=180�㣬��GAB=��DCB��֤����DCB�ա�GAB������֤����DBG�ǵ���ֱ�������Σ�
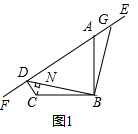
��2����ͼ������C��CN��BD��N�����ɣ�1���á�GDB=45�㣬��BDC=45�㣬����֤����DNC�ǵ���ֱ�������Σ���������ǵ����Ǻ���ֵ�ó���CBD=30�㣬���ɵó�CN��DN��BN=$\sqrt{3}$�������BD���ɣ�
��3�����ݡ�DBG�ǵ���ֱ�������Σ���ABC=90�㣬��GBD=90�㣬�ó���ABG=��DBC����֤����C=��HAB����֤��AGB�ա�CDB���á�DCG�ǵ��������Σ��Ӷ��ó���ֱ��EF�����Ƶ�A����ʱ�뷽����ת��ͼ3��λ��ʱ��BD=BG��
���  �⣺��1���ߡ�ABC=90�㣬GB��DB��
�⣺��1���ߡ�ABC=90�㣬GB��DB��
���ABD+��DBC=90�㣬��ABD+��GBA=90�㣬
���DBC=��GBA��
���ı��ε��ڽǺ͵���360�㣬
��CD��EF��ABC=90�㣬
���DAB+��DBC=180�㣬
�ߡ�DAB+��GAB=180�㣬
���GAB=��DCB��
�ڡ�DCB�͡�GAB�У�$\left\{\begin{array}{l}{��DBC=��GBA}\\{AB=BC}\\{��DCB=��GAB}\end{array}\right.$��
���DCB�ա�GAB����BD=BG��
��GB��DB��
���DBG�ǵ���ֱ�������Σ�
��2����ͼ������C��CN��BD��N��
�ߡ�DBG�ǵ���ֱ�������Σ�
���GDB=45�㣬
��CD��EF��
���BDC=45�㣬
���DNC�ǵ���ֱ�������Σ�
��tan��CBD=$\frac{\sqrt{3}}{3}$��
���CBD=30�㣬
��BC=2��
��CN=1��
��DN=1��BN=$\sqrt{3}$��
��BD=BN+DN=1+$\sqrt{3}$��
��3���ߡ�DBG�ǵ���ֱ�������Σ���ABC=90�㣬��GBD=90�㣬
���ABG+90��=��CBG����DBC+90��=��CBG��
���ABG=��DBC��
��CD��EF��
���C+��CHD=90�㣬
���ڡ�AHB�У���ABH=90�㣬
���HAB+��AHB=90�㣬
��CHD=��AHB�����C=��HAB��
�֡�AB=CB��
���AGB�ա�CDB��
��BD=BG��
��DCG�ǵ��������Σ�
�൱ֱ��EF�����Ƶ�A����ʱ�뷽����ת��ͼ3��λ��ʱ��BD=BG��
���� ���⿼���˼��α任�ۺ��⣬ȫ�������ε����ʺ��ж�������ȫ�����������ó����߶�����ǽ������ij��÷���������Ĺؼ���ѧ�����Ӹ����ߣ�����ȫ�������ν�����⣬�DZ����ͻ�Ƶ㣬��Ŀ�Ƚ��ѣ������п�ѹ���⣮


 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
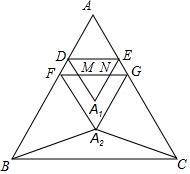 ��ͼ����֪�ȱߡ�ABC�У�DE��BC��FG��BC���ֽ��ȱߡ�ABC�ֱ���DE��FG���ۣ���A�ֱ����ڵ�A1�͵�A2������A2B��A2C��
��ͼ����֪�ȱߡ�ABC�У�DE��BC��FG��BC���ֽ��ȱߡ�ABC�ֱ���DE��FG���ۣ���A�ֱ����ڵ�A1�͵�A2������A2B��A2C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
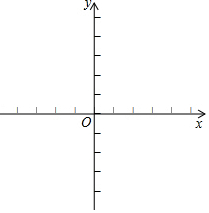 ��ƽ��ֱ������ϵxOy�У�������y=mx2-2mx+m-2��m��0����x��Ľ���ΪA��B��
��ƽ��ֱ������ϵxOy�У�������y=mx2-2mx+m-2��m��0����x��Ľ���ΪA��B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
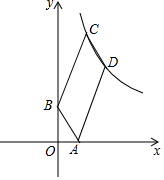 ��ͼ����֪�ı���ABCD��ƽ���ı��Σ�AD=2AB��A��B���������ֱ�Ϊ
��ͼ����֪�ı���ABCD��ƽ���ı��Σ�AD=2AB��A��B���������ֱ�Ϊ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���OABC�DZ߳�Ϊ2�������Σ���PΪOA��������һ�㣨���O��A���غϣ�������CP������P��PM��CP��AB�ڵ�D����PM=CP������M��MN��OA����BO�ڵ�N������ND��BM����OP=t��
��ͼ���ı���OABC�DZ߳�Ϊ2�������Σ���PΪOA��������һ�㣨���O��A���غϣ�������CP������P��PM��CP��AB�ڵ�D����PM=CP������M��MN��OA����BO�ڵ�N������ND��BM����OP=t���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com