
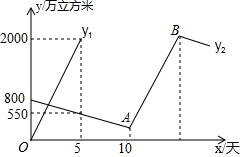
 因南方旱情严重,乙水库的蓄水量以每天相同的速度持续减少,为缓解旱情,北方甲水库立即以管道运输的方式给予支援,如图是乙水库的蓄水量y1(单位:万立方米)关于时间x(单位:天)的函数图象和甲水库输水量y1(单位:万立方米)关于时间x(0≤x≤5)的函数图象,在单位时间内、甲水库的放水量与乙水库的进水量相同(水在排放、接收以及输送过程中的损耗不计),通过分析图象解答下列问题:
因南方旱情严重,乙水库的蓄水量以每天相同的速度持续减少,为缓解旱情,北方甲水库立即以管道运输的方式给予支援,如图是乙水库的蓄水量y1(单位:万立方米)关于时间x(单位:天)的函数图象和甲水库输水量y1(单位:万立方米)关于时间x(0≤x≤5)的函数图象,在单位时间内、甲水库的放水量与乙水库的进水量相同(水在排放、接收以及输送过程中的损耗不计),通过分析图象解答下列问题:分析 (1)设y1=k′x(0≤x≤5),把点(5,2000)坐标代入求出k′的值即可;
(2)由图象可以看出,10天后乙水库蓄水量开始增加,由直线AB′的函数解析式得出A点坐标,求出此时乙水库的蓄水量;
(3)要求直线AB的解析式需求出B点坐标,甲的排水量为乙的进水量,则B的横坐标为15,按等量关系“15天后乙的蓄水量=10天原有的水量+甲注入的水量-自身排出的水量”求出B点纵坐标,再求出函数解析式.
解答 解:(1)设y1=k′x(0≤x≤5),把点(5,2000)代入得:k′=400,
∴设y1=400x(0≤x≤5);
(2)由函数图象可知:甲水库输出的水第10天时开始注入乙水库,
设直线A′B的解析式为:y=kx+b,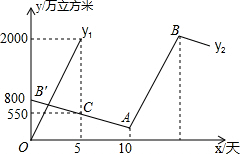
∵B(0,800),C(5,550)
∴$\left\{\begin{array}{l}{b=800}\\{5k+b=550}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{k=-50}\\{b=800}\end{array}\right.$,
∴直线AB′的解析式为:yAB′=-50x+800(0≤x≤10),
当x=10时,y=300
∴此时乙水库的蓄水量为300(万米3).
答:在第10天时甲水库输出的水开始注入乙水库,此时乙水库的蓄水量为300万立方米.
(3)∵甲水库单位时间的放水量与乙水库单位时间的进水量相同且损耗不计,
∴乙水库的进水时间为5天,
∵乙水库15天后的蓄水量为:300+2000-5×50=2050(万米3),
∵过点A的直线解析式为yAB′=-50x+800,
∴当x=10时,y=-500+800=300,
∴A(10,300),B(15,2050)
设直线AD的解析式为:y=k1x+b1,
∴$\left\{\begin{array}{l}{10{k}_{1}+{b}_{1}=300}\\{15{k}_{1}+{b}_{1}=2050}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{k}_{1}=350}\\{{b}_{1}=-3200}\end{array}\right.$,
∴直线AB的解析式为:yAB=350x-3200(10≤x≤15).
点评 本题考查了函数图象与实际结合的问题,同学们要具备读图的能力,能够运用一次函数解决实际问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在平行四边形ABCD中,BC=6cm,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形.求:
如图,在平行四边形ABCD中,BC=6cm,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形.求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
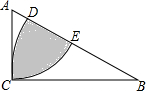 如图,在Rt△ABC中,∠A=60°,AB=2,以点B为圆心,BC为半径的弧交AB于点D,以点A为圆心,AC为半径的弧交AB于点E,则图中阴影部分的面积为$\frac{5π-6\sqrt{3}}{12}$.
如图,在Rt△ABC中,∠A=60°,AB=2,以点B为圆心,BC为半径的弧交AB于点D,以点A为圆心,AC为半径的弧交AB于点E,则图中阴影部分的面积为$\frac{5π-6\sqrt{3}}{12}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com