
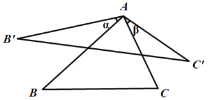
【题目】如图,将△ABC的边AB绕着点A顺时针旋转![]() (
(![]() )得到AB′,边AC绕着点A逆时针旋转
)得到AB′,边AC绕着点A逆时针旋转![]() (
(![]() )得到AC′,联结B′C′,当
)得到AC′,联结B′C′,当![]() +
+![]() =60°时,我们称
=60°时,我们称![]() AB′C′是
AB′C′是![]() ABC的“双旋三角形”,如果等边
ABC的“双旋三角形”,如果等边![]() ABC的边长为a, 那么它所得的“双旋三角形”中B′C′=___________(用含a的代数式表示).
ABC的边长为a, 那么它所得的“双旋三角形”中B′C′=___________(用含a的代数式表示).
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于G,连接AG、HG.下列结论:①CE⊥DF;②AG=DG;③∠CHG=∠DAG;④2HG=AD.正确的有( )
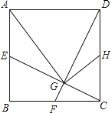
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,同时将点A(﹣1,0)、B(3,0)向上平移2个单位长度再向右平移1个单位长度,分别得到A、B的对应点C、D.连接AC,BD

(1)求点C、D的坐标,并描出A、B、C、D点,求四边形ABDC面积;
(2)在坐标轴上是否存在点P,连接PA、PC使S△PAC=S四边形ABCD?若存在,求点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
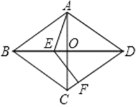
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,点E是线段BO上的一个动点(可以与O、B重合),点F为射线DC上一点,若∠ABC=60,∠AEF=120,AB=5,则EF的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,三角形![]() (记作
(记作![]() )在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是
)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是![]() ,
,![]() ,
,![]() ,先将
,先将![]() 向上平移3个单位长度,再向右平移2个单位长度,得到
向上平移3个单位长度,再向右平移2个单位长度,得到![]() .
.

(1)在图中画出![]() ;
;
(2)点![]() ,
,![]() 的坐标分别为______、______;
的坐标分别为______、______;
(3)若![]() 轴有一点
轴有一点![]() ,使
,使![]() 与
与![]() 面积相等,求出
面积相等,求出![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
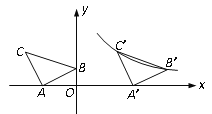
【题目】如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(-2,0),B(0,1).
(1)点C的坐标是 ;
(2)将△ABC沿x轴正方向平移得到△A′ B′C′,且B,C两点的对应点B′,C′恰好落在反比例函数![]() 的图象上,求该反比例函数的解析式.
的图象上,求该反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天水某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两行环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元,
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1220万元,且确保这10辆公交车在该线路的年均载客量总和不少于650万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】媒体报道,近期“手足口病”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所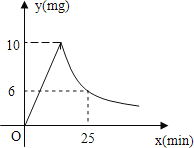
示(即图中线段OA和双曲线在A点及其右侧的部分),根据图象所示信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的函数关系式及自变量的取值范围;
(2)据测定,当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在多长时间内,师生不能进入教室?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列叙述正确的是( )
A. “如果a,b是实数,那么a+b=b+a”是不确定事件
B. “某班50位同学中恰有2位同学生日是同一天”是随机事件
C. 为了了解一批炮弹的杀伤力,采用普查的调查方式比较合适
D. 某种彩票的中奖概率为![]() ,是指买7张彩票一定有一张中奖
,是指买7张彩票一定有一张中奖
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com