Question

已知关于x的方程a²x²+（2a－1）x+1=0有两个实数根x₁，x₂．（1）当a为何值时，x₁≠x₂；（2）是否存在实数a，使方程的两个实数根互为相反数？如果存在，求出a的值；如果不存在，说明理由．
解：（1）根据题意，得△=（2a－1）²－4a²>0，解得a<．
∴当a<时，方程有两个不相等的实数根．
（2）存在，如果方程的两个实数根x₁，x₂互为相反数，则x₁+x₂=－=0①，
解得a=，经检验，a=是方程①的根．
∴当a=时，方程的两个实数根x₁与x₂互为相反数．
上述解答过程是否有错误？如果有，请指出错误之处，并解答．

Answer 1

有错误

解析试题分析：（1）根据根的判别式结合一元二次方程的二次项系数不为0即可作出判断；
（2）根据a=不符合（1）中得到的a的范围即可作出判断.
（1）若方程有两个不相等实数根，则方程首先满足是一元二次方程，
∴a²≠0且满足（2a－1）²－4a²>0，
∴a<且a≠0；
（2）a不可能等于  
∵（1）中求得方程有两个不相等实数根，同时a的取值范围是a<且a≠0，
而a=>不符合题意，所以不存在这样的a值，使方程的两个实数根互为相反数
考点：一元二次方程根的判别式
点评：解题的关键是熟记一元二次方程根的情况与判别式△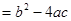的关系：（1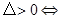）方程有两个不相等的实数根；（2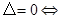）方程有两个相等的实数根；（3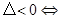）方程没有实数根．