
| 11 | 10 | 6 | 15 | 9 | 16 | 13 | 12 | 0 | 8 | 2 | 8 | 10 | 17 | 6 |
| 13 | 7 | 5 | 7 | 3 | 12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
分析 (1)由抽取30个符合年龄条件的青年人中A级的有15人,即可求得样本数据中为A级的频率;
(2)根据题意得:1000个18~35岁的青年人中“日均发微博条数”为A级的人数为:1000×$\frac{1}{2}$=500;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与抽得2个人的“日均发微博条数”都是3的情况,再利用概率公式求解即可求得答案.
解答 解:(1)∵抽取30个符合年龄条件的青年人中A级的有15人,
∴样本数据中为A级的频率为:15÷30=0.5;
(2)1000个18~35岁的青年人中“日均发微博条数”为A级的人数为:1000×0.5=500(人);
(3)C级的有:0,2,3,3四人,
画树状图得: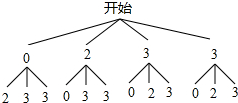
∵共有12种等可能的结果,抽得2个人的“日均发微博条数”都是3的有2种情况,
∴抽得2个人的“日均发微博条数”都是3的概率为:$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查的是用列表法或画树状图法求概率、用频率估计概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:解答题
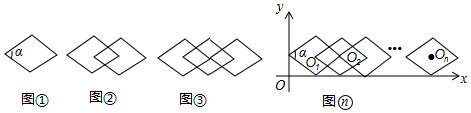
| 图形名称 | 基本图形的个数 | 菱形的个数 |
| 图① | 1 | 1 |
| 图② | 2 | 3 |
| 图③ | 3 | 7 |
| 图④ | 4 | 11 |
| … | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
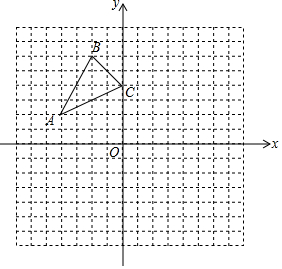 如图,已知A (-4,2),B (-2,6),C (0,4)是直角坐标系平面上三点.
如图,已知A (-4,2),B (-2,6),C (0,4)是直角坐标系平面上三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
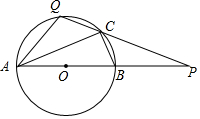 已知如图:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q是半圆上一动点(不与A、B重合),连接PQ,交⊙O于点C.下列结论:①∠QAP=∠BCP;②$\frac{CP}{QP}$=$\frac{BP}{AP}$;若点Q为劣弧$\widehat{AC}$的中点,则C是PQ的中点;④若点Q与C重合时,则PQ=2$\sqrt{3}$.其中正确的是①③④0(把所有正确结论的序号都选上)
已知如图:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q是半圆上一动点(不与A、B重合),连接PQ,交⊙O于点C.下列结论:①∠QAP=∠BCP;②$\frac{CP}{QP}$=$\frac{BP}{AP}$;若点Q为劣弧$\widehat{AC}$的中点,则C是PQ的中点;④若点Q与C重合时,则PQ=2$\sqrt{3}$.其中正确的是①③④0(把所有正确结论的序号都选上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示.在?ABCD中.E、F分别是边AD、BC上的点,连接AF、BE交于点G:连接CE、DF交于点H,连接GH.
如图所示.在?ABCD中.E、F分别是边AD、BC上的点,连接AF、BE交于点G:连接CE、DF交于点H,连接GH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com