
【题目】对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=![]() ,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________.
,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________.
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】三角形ABC的三条内角平分线为AE、BF、CG,下面的说法中正确的个数有( )
①△ABC的内角平分线上的点到三边距离相等
②三角形的三条内角平分线交于一点
③三角形的内角平分线位于三角形的内部
④三角形的任一内角平分线将三角形分成面积相等的两部分.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,则不难证明S1=S2+S3 .
(1) 如图②,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,那么S1、S2、S3之间有什么关系?(不必证明)
(2) 如图③,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1、S2、S3之间的关系并加以证明;
(3) 若分别以直角三角形ABC三边为边向外作三个正多边形,其面积分别用S1、S2、S3表示,请你猜想S1、S2、S3之间的关系?.

查看答案和解析>>
科目:初中数学 来源: 题型:
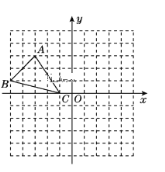
【题目】如图,已知网格上最小的正方形的边长为1,
(1)作△ABC关于![]() 轴的对称图形△A'B'C'(不写做法),并写出A'B'C'的坐标,想一想:关于
轴的对称图形△A'B'C'(不写做法),并写出A'B'C'的坐标,想一想:关于![]() 轴对称的两个点之间有什么关系?
轴对称的两个点之间有什么关系?
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某电脑公司有A型、B型、C型三种型号的电脑,其价格分别为A型每台6 000元,B型每台4 000元,C型每台2 500元,我市东坡中学计划将100 500元钱全部用于该电脑公司购进其中两种不同型号的电脑共36台,请你设计出几种不同的购买方案供该校选择,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com