
【题目】背景资料:
在已知△ABC所在平面上求一点P,使它到三角形的三个顶点的距离之和最小.
这个问题是法国数学家费马1640年前后向意大利物理学家托里拆利提出的,所求的点被人们称为“费马点”.
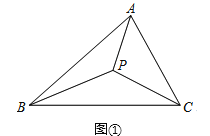
如图①,当△ABC三个内角均小于120°时,费马点P在△ABC内部,此时∠APB=∠BPC=∠CPA=120°,此时,PA+PB+PC的值最小.
解决问题:
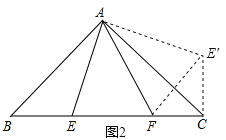
(1)如图②,等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.
为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA,PB,PC转化到一个三角形中,从而求出∠APB= ;
基本运用:
(2)请你利用第(1)题的解答思想方法,解答下面问题:
如图③,△ABC中,∠CAB=90°,AB=AC,E,F为BC上的点,且∠EAF=45°,判断BE,EF,FC之间的数量关系并证明;
能力提升:
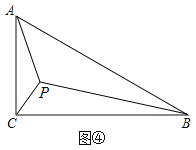
(3)如图④,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点P为Rt△ABC的费马点,
连接AP,BP,CP,求PA+PB+PC的值.

【答案】(1)150°;
(2)E′F2=CE′2+FC2,理由见解析;
(3)![]() .
.
【解析】试题分析:(1)
(2)首先把△ACE绕点A顺时针旋转90°,得到△ACE′.连接E′F,由旋转的性质得,AE′=AE,CE′=BE,∠CAE′=∠BAE,∠ACE′=∠B,∠EAE′=90°,然后再证明△EAF≌△E′AF可得E′F=EF,,再利用勾股定理可得结论;
(3)将△AOB绕点B顺时针旋转60°至△A′O′B处,连接OO′,根据已知证明C、O、A′、O′四点共线,在Rt△A′BC中,利用勾股定理求得A′C的长,根据新定义即可得OA+OB+OC =![]() .
.
试题解析:(1)∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∴将△ABP绕顶点A逆时针旋转60°得到△ACP′,如图,连结PP′,
∴AP=AP′=3,∠PAP′=60°,P′C=PB=4,∠APB=∠AP′C,
∴△APP′为等边三角形,
∴∠PP′A=60°,PP′=AP=3,
在△PP′C中,∵PP′=3,P′C=4,PC=5,
∴PP′2+P′C2=PC2,
∴△PP′C为直角三角形,∠PP′C=90°,
∴∠AP′C=∠PP′A+∠PP′C=60°+90°=150°,
∴∠APB=150°,
故答案为:150°;
(2)E′F2=CE′2+FC2,理由如下:
如图2,把△ABE绕点A逆时针旋转90°得到△ACE′,
由旋转的性质得,AE′=AE,CE′=BE,∠CAE′=∠BAE,∠ACE′=∠B,∠EAE′=90°,
∵∠EAF=45°,
∴∠E′AF=∠CAE′+∠CAF=∠BAE+∠CAF=∠BAC﹣∠EAF=90°﹣45°=45°,
∴∠EAF=∠E′AF,
在△EAF和△E′AF中,  ,
,
∴△EAF≌△E′AF(SAS),
∴E′F=EF,
∵∠CAB=90°,AB=AC,
∴∠B=∠ACB=45°,
∴∠E′CF=45°+45°=90°,
由勾股定理得,E′F2=CE′2+FC2,即EF2=BE2+FC2;
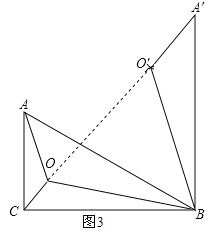
(3)如图3,将△AOB绕点B顺时针旋转60°至△A′O′B处,连接OO′,
∵在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,∴AB=2,
∴BC=![]() =
=![]() ,
,
∵△AOB绕点B顺时针方向旋转60°,∴△A′O′B如图所示;
∠A′BC=∠ABC+60°=30°+60°=90°,
∵∠C=90°,AC=1,∠ABC=30°,∴AB=2AC=2,
∵△AOB绕点B顺时针方向旋转60°,得到△A′O′B,
∴A′B=AB=2,BO=BO′,A′O′=AO,
∴△BOO′是等边三角形,
∴BO=OO′,∠BOO′=∠BO′O=60°,
∵∠AOC=∠COB=∠BOA=120°,
∴∠COB+∠BOO′=∠BO′A′+∠BO′O=120°+60°=180°,
∴C、O、A′、O′四点共线,
在Rt△A′BC中,A′C=![]() =
=![]() =
=![]() ,
,
∴OA+OB+OC=A′O′+OO′+OC=A′C=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】坐火车从上海到娄底,高铁G1329次列车比快车K575次列车少需要9小时,已知上海到娄底的铁路长约1260千米,G1329的平均速度是K575的2.5倍.
(1)求K575的平均速度;
(2)高铁G1329从上海到娄底只需几小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国倡导的“一带一路”建设将促进我国与世界各国的互利合作.根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
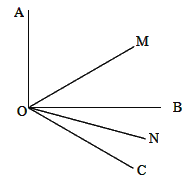
【题目】如图,∠AOB=90°,∠BOC=60°,射线OM平分∠AOC,ON平分∠BOC。
(1)求∠MON的度数;
(2)如果(1)中,∠AOB=α,∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(3)从(1)、(2)的结果中,你能得到什么规律?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.内错角相等
B.平面内,过一点有且只有一条直线与已知直线垂直
C.相等的角是对顶角
D.过一点有且只有一条直线与已知直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生会为了解本年级600名学生的睡眠情况,将同学们某天的睡眠时长t(小时)分为A,B,C,D,E(A:9≤t≤24;B:8≤t<9;C:7≤t<8;D:6≤t<7;E:0≤t<6)五个选项,进行了一次问卷调查,随机抽取n名同学的调查问卷并进行了整理,绘制成如下条形统计图,根据统计图提供的信息解答下列问题:
(1)求n的值;
(2)根据统计结果,估计该年级600名学生中睡眠时长不足7小时的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
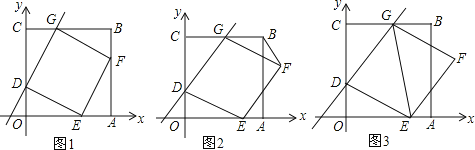
【题目】在平面直角坐标系xOy中,边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,直线y=mx+2与OC,BC两边分别相交于点D,G,以DG为边作菱形DEFG,顶点E在OA边上.
(1)如图1,顶点F在边AB上,当CG=OD时,
求m的值;
菱形DEFG是正方形吗?如果是请给予证明.
(2)如图2,连接BF,设CG=a,△FBG的面积为S,求S与a的函数关系式;
(3)如图3,连接GE,当GD平分∠CGE时,请直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口的直径 EF 长为10cm,母线OE(OF)长为10cm,在母线OF 上的点A 处有一块爆米花残渣且FA=2cm,一只蚂蚁从杯口的点E 处沿圆锥表面爬行到A 点,则此蚂蚁爬行的最短距离为 cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com