练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

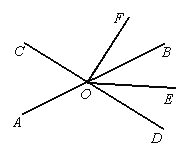
    【题目】如图，直线AB、CD相交于点O，∠AOD＝120°，FO⊥OD，OE平分∠BOD．

    （1）求∠EOF的度数；

    （2）试说明OB平分∠EOF．

    【答案】(1)60°;(2)证明见解析.

    【解析】

    （1）利用邻补角的性质求出∠BOD，再利用角平分线的性质求出∠EOD，由垂直的定义即可得到结论；

    （2）由垂直和∠BOD的度数可求出∠FOB，然后与∠BOE比较即可得出结论．

    （1）∵AB为一直线，∠AOD=120°，∴∠BOD=60°．

    ∵OE平分∠BOD，∴∠EOD=∠EOB =∠DOB= 30°．

    ∵OF⊥OD，∴∠FOD=90°，∴∠EOF＝∠FOD ∠EOD＝90°30°＝60°．

    （2）∵∠FOD=90°，∠BOD=60°，∴∠FOB＝∠FOD∠BOD＝90°60°＝30°．

    ∵∠BOE＝30°，∴∠BOF＝∠BOE，∴OB平分∠EOF．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一个几何体及它的表面展开图如图所示．（几何体的上、下底面均为梯形）
    （1）写出这个几何体的名称；
    （2）计算这个几何体的侧面积和左视图的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知多项式2x2+x3+x﹣5x4﹣．

    (1)请指出该多项式是几次几项式，并写出它的二次项、一次项和常数项；

    (2)按要求把这个多项式重新排列：①按x的降幂排列；②按x的升幂排列．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在三角形ABC中，BC=14，AC=9，AB=13，它的内切圆分别和BC、AC、AB切于点D、E、F，那么AF、BD、CE的长分别为（　　）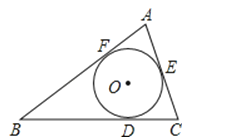

    A.AF=4，BD=9，CE=5
    B.AF=4，BD=5，CE=9
    C.AF=5，BD=4，CE=9
    D.AF=9，BD=4，CE=5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

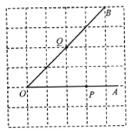
    【题目】如图，点P，Q分别是∠AOB的边OA，OB上的点.

    (1)过点P画OB的垂线，垂足为H；

    (2)过点Q画OA的垂线，交OA于点C，连接PQ；

    (3)线段QC的长度是点Q到 的距离， 的长度是点P到直线OB的距离，因为直线外一点和直线上各点连接的所有线段中，垂线段最短，所以线段PQ、PH的大小关系是 (用“＜”号连接).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F，且∠ACB=90°，AB=5，BC=3，点P是边AC上的一动点，PH⊥AB，垂足为H．
    （1）求⊙O的半径的长及线段AD的长；
    （2）设PH=x，PC=y，求y关于x的函数关系式．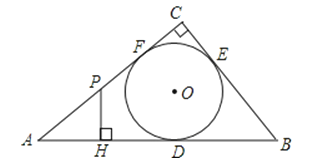

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰△ABC中，CA=CB，AD是腰BC边上的高，△ACD的内切圆⊙E分别与边AD、BC相切于点F、G，连AE、BE．
    （1）求证：AF=BG；
    （2）过E点作EH⊥AB于H，试探索线段EH与线段AB的数量关系，并说明理由．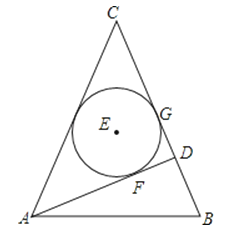

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在数轴上，点A表示-5，点B表示10.动点P从点A出发，沿数轴正方向以每秒1个单位的速度匀速运动;同时，动点Q从点B出发，沿数轴负方向以每秒2个单位的速度匀速运动.设运动时间为t秒.

    (1)当t为 秒时，P，Q两点相遇，求出相遇点所对应的数;

    (2)当t为何值时，P，Q两点的距离为3个单位长度，并求出此时点P对应的数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】A，B两点在数轴上的位置如图所示，O为原点，现A，B两点分别以1个单位长度/秒的速度同时向左运动。

    （1）几秒后，原点恰好在A，B两点正中间？

    （2）几秒后，恰好有OA：OB=1：2.

    查看答案和解析>>

    同步练习册答案