
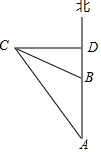
 如图,下午2时一艘轮船从A处向正北方向航行,5时达到B处,继续航行到达D处时发现,灯塔C恰好在正西方向,从A处、B处望灯塔C的角度分别是∠A=30°,∠DBC=60°,已知轮船的航行速度为24海里/时,求AD的长度.
如图,下午2时一艘轮船从A处向正北方向航行,5时达到B处,继续航行到达D处时发现,灯塔C恰好在正西方向,从A处、B处望灯塔C的角度分别是∠A=30°,∠DBC=60°,已知轮船的航行速度为24海里/时,求AD的长度. 分析 首先根据C在D的正西方向,∠A=30°,∠DBC=60°,判断出BC=BA,∠BCD=30°,再根据含30度角的直角三角形的性质,判断出DB=$\frac{1}{2}$CB;然后根据路程=速度×时间,求出AB的长度是多少,即可求出AD的长度是多少.
解答 解:∵C在D的正西方向,
∴∠ADC=90°;
∵∠A=30°,∠DBC=60°,∠DBC=∠A+∠BCA
∴∠BCA=30°,
∴∠BCA=∠A,
∴BC=BA.
在Rt△CBD中,∠DBC=60°,
∴∠BCD=30°,
∴DB=$\frac{1}{2}$CB,
∴AD=AB+DB=AB+$\frac{1}{2}$CB=AB+$\frac{1}{2}$AB=$\frac{3}{2}$AB,
∵AB=24×(5-2)=72(海里),
∴AD=$\frac{3}{2}$AB=$\frac{3}{2}$×72=108(海里).
答:AD的长度是108海里.
点评 此题主要考查了含30度角的直角三角形的性质,方向角的判断,以及行程问题中速度、时间和路程的关系,要熟练掌握.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com