
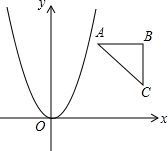
 已知Rt△ABC的顶点坐标为A(1,2),B(2,2),C(2,1),若抛物线y=ax2与该直角三角形无公共点,则a的取值范围是a<0或a>2或0<a<$\frac{1}{4}$.
已知Rt△ABC的顶点坐标为A(1,2),B(2,2),C(2,1),若抛物线y=ax2与该直角三角形无公共点,则a的取值范围是a<0或a>2或0<a<$\frac{1}{4}$. 分析 显然a<0时,抛物线开口向下,与直角三角形无公共点;当a>0时,分别求出抛物线y=ax2经过点A与点C时a的值,然后根据二次函数的性质即可求解.
解答 解:∵抛物线y=ax2与Rt△ABC无公共点,A(1,2),B(2,2),C(2,1),
∴可分两种情况:
①a<0时,抛物线开口向下,与直角三角形无公共点;
②a>0时,
如果y=ax2经过点A,那么a=2,
所以a>2时,抛物线y=ax2与该直角三角形无公共点;
如果y=ax2经过点C,那么4a=1,解得a=$\frac{1}{4}$,
所以0<a<$\frac{1}{4}$时,抛物线y=ax2与该直角三角形无公共点.
综上所述,若抛物线y=ax2与该直角三角形无公共点,则a的取值范围是a<0或a>2或0<a<$\frac{1}{4}$.
故答案为a<0或a>2或0<a<$\frac{1}{4}$.
点评 本题考查了二次函数的性质,用到的知识点:①对于二次函数y=ax2+bx+c(a≠0),当a>0时,抛物线开口向上,x<-$\frac{b}{2a}$时,y随x的增大而减小;x>-$\frac{b}{2a}$时,y随x的增大而增大;x=-$\frac{b}{2a}$时,y取得最小值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最低点.②|a|越大,开口越小;|a|越小,开口越大.


科目:初中数学 来源: 题型:填空题
 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为122°.
如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为122°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿着过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长等于5π.(结果保留π)
如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿着过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长等于5π.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
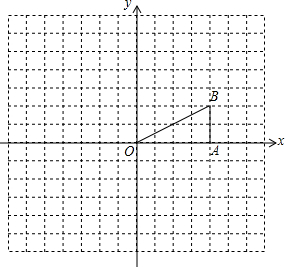 如图,在Rt△OAB中,∠OAB=90°,且B点的坐标为(4,2).
如图,在Rt△OAB中,∠OAB=90°,且B点的坐标为(4,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 4 | D. | -4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com